Tham Khảo:

https://olm.vn/hoi-dap/detail/86010246553.html

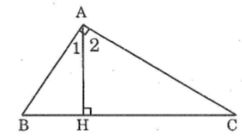
Có thể tìm góc B bằng hai cách:

Cách 1

Ta có: ∠(A1 ) + ∠(A2 ) = ∠(BAC) = 90o(1)

Vì ΔAHB vuông tại H nên:

∠B + ∠(A1) = 90o(tính chất tam giác vuông) (2)

Từ (1) và (2) suy ra ∠B = ∠(A2 )

Cách 2

Vì ΔABC vuông tại A nên:

∠B +∠C = 90o (theo tính chất tam giác vuông) (1)

Vì ΔAHC vuông tại H nên:

∠(A2 ) + ∠C = 90o (tính chất tam giác vuông) (2)

Từ (1) và (2) suy ra: ∠B = ∠(A2)

Ta có:

góc BAH + góc HAC= 90độ (tam giác ABC vuông tại H)

Mà góc BAH + góc ABH =90độ (tam giác ABH vuông tại H)

=>góc ABH= góc HAC

Vậy góc B = góc HAC

cái tam giác mik vẽ là tam giác vuông cân nên góc B = góc C

nếu là tam giác thường thì khi đó:
kẻ đường thẳng sog song với AB đí qua H cắt AC tại K ( theo hibhf vẽ)

khi đó theo tính chất 2 đường thẳng song song sẽ có HK // BA

mà BA vuông góc tại AC( tam giác ABC vuông tại A)

=> HK vuông góc với AC

theo tính chất đồng vị  => góc B = góc CHK

a) Sửa đề: Trên HC lấy E sao cho HE=HB và c/m ΔBHA=ΔEHA

Xét ΔBHA vuông tại H và ΔEHA vuông tại H có 

AH chung

BH=EH(gt)

Do đó: ΔBHA=ΔEHA(hai cạnh góc vuông)

a) Sửa đề: Trên HC lấy E sao cho HE=HB 

tam giác BHA=tam giác EHA(c.g.c)

tam giác BDA=tam giác BDE(ch-gn)

suy ra góc A=góc E=90 độ và AD=ED

suy ra DE vuông góc với BC 

Áp dung định lí pitago vào tam giác DEC có góc E=90 độ

DC^2=DE^2+CE^2

suy ra DC > DE

mà DE = DA 

suy ra DC>DA

Hình tự vẽ

Xét tam giác ABC có \(\widehat{A}=90^o=>\widehat{B}+\widehat{C}=90^o\)

Xét tam giác HAC có \(\widehat{AHC}=90^o=>\widehat{C}+\widehat{HAC}=90^o\)

Từ 2 điều trên => \(\widehat{B}=\widehat{HAC}\)

có làm thì mới có ăn

Bạn xem lời giải bài tương tự tại đường link dưới nhé:

Câu hỏi của Nguyễn Ngọc Vy - Toán lớp 7 - Học toán với OnlineMath