Điều kiện cần và đủ để z là một số thực là:
A. z = z ¯ .
B. z = z .
C. z = − z ¯ .
D. z = − z .
Điều kiện cần và đủ để z là một số thực là:
A. z = z
B. z = z
C. z = - z
D. z = - z
Cho hai số phức z = a + bi và z’ = a’ + b’i . Tìm điều kiện giữa a; b; a’; b’ để z + z’ là một số thuần ảo.
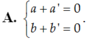
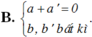
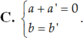
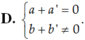
Chọn D.
Ta có: z + z’ = (a + a’) + (b + b’)i là số thuần ảo 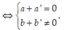
Có bao nhiêu số phức có phần thực và phần ảo là các số nguyên, đồng thời thỏa các điều kiện z + 4 i + z - 6 i = z + i + z - 3 i và z ≤ 2019 ?
A. 2019
B. 7857
C. 4030
D. 4032
Gọi S là tập hợp các số phức z có phần thực và phần ảo đều là các số nguyên đồng thời thoả mãn hai điều kiện: z - 3 - 4 i ≤ 2 và z + z ¯ ≤ z - z ¯ . Số phần tử của tập S bằng
A. 11.
B. 12.
C. 13.
D. 10.
Trong các số phức z thỏa mãn điều kiện z − 2 − 4 i = z − 2 i . Số phức z có môđun nhỏ nhất có tổng phần thực và phần ảo là
A. 0.
B. 4.
C. 3.
D. 2.
Trong các số phức z thỏa mãn điều kiện z - 2 - 4 i = z - 2 i Số phức z có môđun nhỏ nhất có tổng phần thực và phần ảo là
A. 0.
B. 4.
C. 3.
D. 2.
Có tất cả bao nhiêu số thực m để có duy nhất một số phức z thoả mãn đồng thời hai điều kiện: z - 1 + i = m và z - 1 - 13 i ≤ 13
A. 2.
B. 3.
C. 4.
D. 1.
Có tất cả bao nhiêu số thực m để có duy nhất một số phức z thoả mãn đồng thời hai điều kiện: z - 1 + i = m và z - 1 - 3 i ≤ 13
A. 2
B. 3
C. 4
D. 1
Gọi M(z) có ![]() M thuộc đường tròn
C
1
có tâm
M thuộc đường tròn
C
1
có tâm ![]()
Và ![]() thuộc hình tròn
C
2
có tâm
thuộc hình tròn
C
2
có tâm ![]()
Yêu cầu bài toán tương đương với C 1 C 2 có đúng một điểm chung
TH1: C 1 C 2 tiếp xúc ngoài như hình vẽ:
![]()
![]()

TH2: C 1 C 2 tiếp xúc trong như hình vẽ

![]()
![]()
Vậy có hai giá trị của tham số.
Chọn đáp án A.
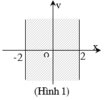
Cho số phức z = a + b i ( a , b ∈ R ) . Để điểm biểu diễn của z nằm trong dải (-2;2), ở hình 1, điều kiện của a và b là:
A. a , b ∈ - 2 ; 2
B. a ∈ - 2 ; 2 ; b ∈ ℝ
C. a ∈ ℝ ; b ∈ - 2 ; 2
D. a , b ∈ - 2 ; 2
Chọn B.
Các số phức trong dải đã cho có phần thực trong khoảng (-2;2), phần ảo tùy ý