Thể tích của khối cầu nội tiếp hình lập phương có cạnh bằng a 2 là
A. π 2 a 3 6
B. π 2 a 3 3
C. π a 3 3
D. π a 3 6
Thể tích của khối cầu nội tiếp hình lập phương có cạnh bằng
a 2 là
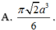
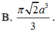
![]()
![]()
Thể tích của khối cầu nội tiếp hình lập phương có cạnh bằng a 2 là
A. π 2 a 3 6
B. π 2 a 3 3
C. π a 3 3
D. π a 3 6
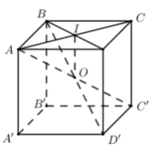
Gọi O là tâm hình lập phương A B C D . A ' B ' C ' D ' . Gọi I là tâm hình vuông ABCD.
Khi đó bán kính mặt cầu nội tiếp hình lập phương A B C D . A ' B ' C ' D ' là R = O I = a 2 2 .
Vậy thể tích khối cầu nội tiếp hình lập phương là:
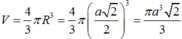
Chọn B.
Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S 1 là diện tích 6 mặt của hình lập phương, S 2 là diện tích xung quanh của hình trụ. Tỉ số S 2 / S 1 bằng:
A. π /6 B. 1/2
C. π /2 D. π
Tính thể tích khối cầu nội tiếp hình lập phương cạnh a (khối cầu tiếp xúc với tất cả các mặt của hình lập phương).
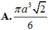
![]()
![]()
![]()
Tính thể tích khối cầu nội tiếp hình lập phương cạnh a (khối cầu tiếp xúc với tất cả các mặt của hình lập phương).
A. π a 3 2 6
B. π a 3 6
C. π a 3 8
D. π a 3 6
Cho hình hình lập phương cạnh a. Thể tích khối cầu nội tiếp hình lập phương là
![]()
![]()
![]()
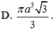
Một hình lập phương có cạnh bằng 2a vừa nội tiếp hình trụ (T) vừa nội tiếp mặt cầu (C) và hai đáy của hình lập phương nằm trên 2 đáy của hình trụ. Tính tỉ số thể tích V c V T giữa khối cầu và khối trụ giới hạn bởi (C) và (T) ?
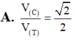
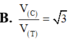
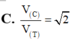
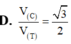
Một hình lập phương có cạnh bằng 2a vừa nội tiếp hình trụ (T) vừa nội tiếp mặt cầu (C) và hai đáy của hình lập phương nằm trên 2 đáy của hình trụ. Tính tỉ số thể tích V C V T giữa khối cầu và khối trụ giới hạn bởi (C) và (T) ?
A. V C V T = 2 2
B. V C V T = 3
C. V C V T = 2
D. V C V T = 3 2
Đáp án là B.
+ Ta có: R C = a 3 ⇒ V C = 4 3 π .3 3 a 3 = 4 π a 3 3 .
+ R T = a 2 ⇒ V T = 2 a .. π 2 a 2 = 4 π a 3
Vậy V C V T = 3 .
Một hình lập phương cạnh bằng a nội tiếp khối cầu ( S 1 ) và ngoại tiếp khối cầu ( S 2 ) , gọi V 1 và V 2 lần lượt là thể tích của các khối S 1 và ( S 2 ) . Tính tỉ số k = V 1 V 2
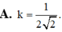
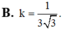
![]()
![]()