\(y=\dfrac{x^2+mx+1}{x+m}=x+\dfrac{1}{x+m}\)

\(\left\{{}\begin{matrix}y'\left(2\right)=0\\y''\left(2\right)< 0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}1-\dfrac{1}{\left(2+m\right)^2}=0\\\dfrac{2}{\left(m+2\right)^3}< 0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}m=-3\\m< -2\end{matrix}\right.\)

Chọn a

Đồ thị hàm số song song với đường thẳng \(y=mx+2\)khi

\(\Rightarrow\hept{\begin{cases}2m-3=m\\2\ne2\left(voli\right)\end{cases}}\Rightarrow2m-m=3\Rightarrow m=3\)

vậy \(m=3\)thì đồ thị hàm số trên song song với đường thẳng \(y=mx+2\)

Chọn D

Để hàm số đạt cực đại x = 1 thì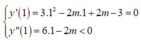  

⇔ m > 3

a) Ta có: \(y=\sqrt{m-3}\cdot x+\dfrac{2}{3}\left(m\ge3\right)\) 

Để đây là hàm số bậc nhất thì: \(\sqrt{m-3}\ne0\Leftrightarrow m=3\) 

Do: \(\sqrt{m-3}\ge0\forall m\ge3\) 

Nên với \(m\ge3\) thì y đồng biến trên R 

b) Ta có: \(y=\dfrac{\sqrt{m}+\sqrt{5}}{\sqrt{m}-\sqrt{5}}\cdot x+2010\left(m\ge0;m\ne5\right)\)

Để đây là hàm số bậc nhất thì: \(\sqrt{m}-\sqrt{5}\ne0\Leftrightarrow\left\{{}\begin{matrix}m\ge0\\m\ne5\end{matrix}\right.\) 

Do \(\sqrt{m}+\sqrt{5}>0\Rightarrow\sqrt{m}-\sqrt{5}< 0\Leftrightarrow m< 5\)

Vậy với 0 ≤ m < 5 thì y nghịch biến trên R

a) Để hàm số là hàm số bậc nhất thì:

√(m - 3) > 0

⇔ m - 3 > 0

⇔ m > 3

Vậy với m > 3 thì hàm số đã cho là hàm bậc nhất

b) Để hàm số là hàm bậc nhất thì √m - √5 ≠ 0 và m ≥ 0

⇔ √m ≠ √5

⇔ m ≠ 5

Vậy m ≠ 5 và m ≥ 0 thì hàm số đã cho làm hàm số bậc nhất

*) Để hàm số ở câu a là hàm đồng biến thì m > 3

*) Để hàm số ở câu b là hàm nghịch biến thì √m < √5

⇔ 0 \(\le\) m < 5

Vậy 0 \(\le\) m < 5 thì hàm số ở câu b là hàm số nghịch biến

Đáp án đúng : A

a) khi m khác 1/2

b)khi m >1

c) khi K<5

a: Để hàm số y=(m+6)x-7 đồng biến thì m+6>0

=>m>-6

b: Để hàm số y=(-k+9)x+100 nghịch biến thì -k+9<0

=>-k<-9

=>k>9

c: Để hai đồ thị hàm số y=12x+(5+m) và y=-3x+(3-m) cắt nhau tại một điểm trên trục tung thì

\(\left\{{}\begin{matrix}m+5=3-m\\12\ne-3\left(đúng\right)\end{matrix}\right.\)

=>m+5=3-m

=>2m=-2

=>m=-1

\(a,\Leftrightarrow3m-1=m+3\Leftrightarrow2m=4\Leftrightarrow m=2\\ b,\Leftrightarrow3m-1\ne m+3\Leftrightarrow m\ne2\)

Hai hàm số nghịch biến khi:

\(\left[{}\begin{matrix}m-1< 0\\m+6< 0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m< 1\\m< -6\end{matrix}\right.\)