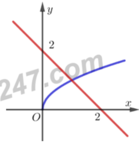
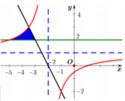
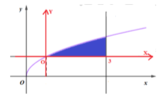
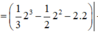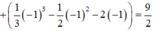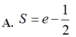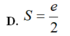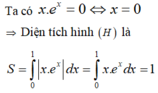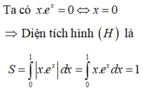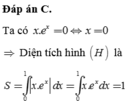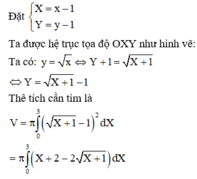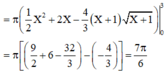Cho (H) là hình phẳng giới hạn bởi đồ thị hàm số
y
=
-
e
x
+
4
x
, trục hoành và hai đường thẳng x=1, x=2; ![]() là thể tích của khối tròn xoay thu được khi quay hình
là thể tích của khối tròn xoay thu được khi quay hình ![]() quanh trục hoành. Khẳng định nào sau đây đúng?
quanh trục hoành. Khẳng định nào sau đây đúng?
A. ![]() .
.
B. 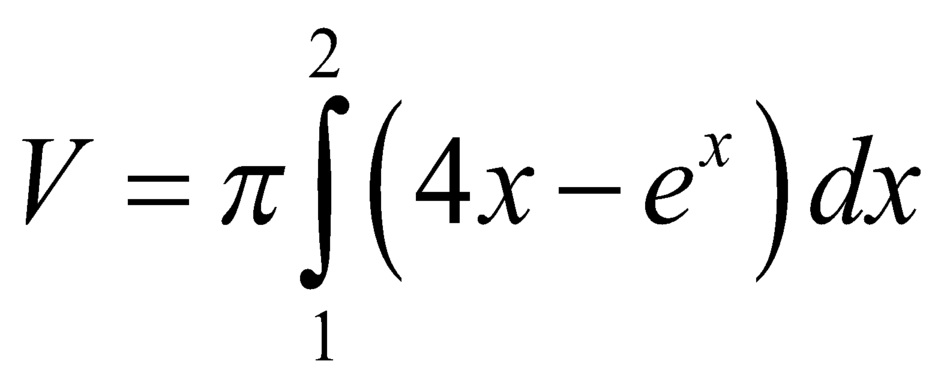 .
.
C. ![]() .
.
D. 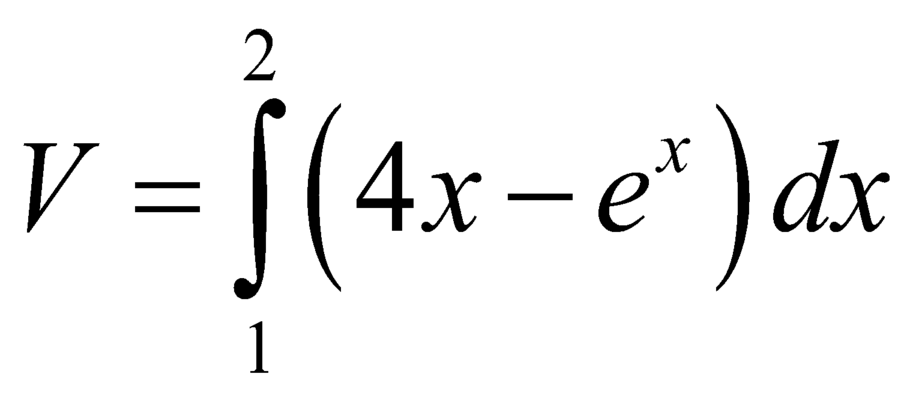 .
.