Trong không gian Oxyz, cho hai đường thẳng d : x = - 1 - 2 t y = t z = - 1 + 3 t d ' : x = 2 + t ' y = - 1 + 2 t ' z = - 2 t ' và mặt phẳng (P): x+y+yz+2=0. Đường thẳng vuông góc với mặt phẳng (P) và cắt hai đường thẳng d, d' có phương trình là:
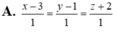
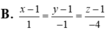


Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng 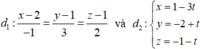 . Phương trình đường thẳng d nằm trong (α): x + 2y - 3z - 2 = 0 và cắt hai đường thẳng d1;d2 là:
. Phương trình đường thẳng d nằm trong (α): x + 2y - 3z - 2 = 0 và cắt hai đường thẳng d1;d2 là:
A. x + 3 5 = y - 2 - 1 = z - 1 1
B. x + 3 - 5 = y - 2 1 = z - 1 - 1
C. x - 3 - 5 = y + 2 1 = z + 1 - 1
D. x + 8 1 = y - 3 3 = z - 4
Trong không gian Oxyz, cho hai đường thẳng và . Phương trình mặt phẳng chứa đường thẳng d: x - 1 2 = y + 1 1 = z - 2 2 và tạo với đường thẳng d’: x + 1 1 = y 2 = z - 1 1 một góc lớn nhất là.
A. x-z+1=0
B. x-4y+z-7=0
C. 3x-2y-2x-1=0
D. –x+4y-z-7=0
Trong không gian Oxyz cho hai đường thẳng d và d’ có phương trình lần lượt là x - 2 2 = y + 4 3 = 1 - z 2 ; x = 4 t y = - 1 + 6 t z = - 1 + 4 t . Xác định vị trí tương đối của hai đường thẳng d và d’.
A. Song song nhau
B. Trùng nhau
C. Cắt nhau
D. Chéo nhau
Đường thẳng d qua M ( 2;-4;1 ) và có vectơ chỉ phương là u → 2 ; 3 ; 2
Đường thẳng d’ qua M' ( 0;1;-1 ) và có vectơ chỉ phương là u ' → = 4 ; 6 ; 4
Do u → và u ' → cùng phương đồng thời M ∉ d ' nên hai đường thẳng đó song song nhau.
Đáp án A
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d : x 1 = y - 2 = z + 1 1 và d ' : x - 1 - 2 = y - 2 4 = z 2 . Viết phương trình mặt phẳn (Q) chứa hai đường thẳng d và d’.
![]()
![]()
![]()
![]()
Đáp án B.
Ta có: Hai vector chỉ phương của hai đường thẳng là cùng phương nên hai đường thẳng luôn đồng phẳng.
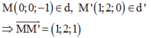
Vector chỉ phương của đường thẳng d là u → = ( 1 ; - 2 ; - 1 )
Vector pháp tuyến của mặt phẳng
![]()
Phương trình mặt phẳng
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d: x 1 = y - 2 = z + 1 1 và d'= x - 1 - 2 ) = y - 2 4 = z 2 . Viết phương trình mặt phẳng (Q) chứa hai đường thẳng d và d’
A. Không tồn tại (Q)
B. (Q): y-2z-2= 0
C. (Q): x-y-2= 0
D. (Q):-2y+4z+1= 0
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d : x - 1 2 = y + 1 1 = z - 2 2 và d ' : x + 1 1 = y 2 = z - 1 1 . Phương trình mặt phẳng chứa đường thẳng d và tạo với đường thẳng d ' một góc lớn nhất là:
![]()
![]()
![]()
![]()
Đáp án B
Nhận xét d và d ' có thể chéo nhau.
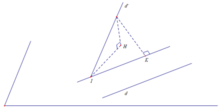
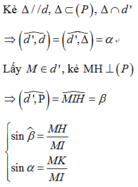
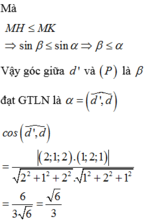

Trong không gian O x y z , cho hai đường thẳng d : x − 1 2 = y + 1 1 = z − 2 2 và d ' : x + 1 1 = y 2 = z − 1 1 . Phương trình mặt phẳng chứa đường thẳng d và tạo với đường thẳng d ' một góc lớn nhất là
A. x − z + 1 = 0 .
B. x − 4 y + z − 7 = 0 .
C. 3 x − 2 y − 2 z − 1 = 0 .
D. − x + 4 y − z − 7 = 0 .
Đáp án B
Nhận xét d và d ' có thể chéo nhau.
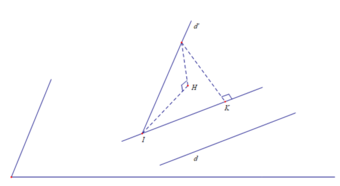
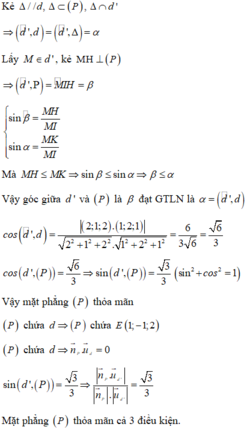
Trong không gian Oxyz, cho hai đường thẳng d : x - 2 4 = y - 6 = z + 1 8 v à d ' : x - 7 - 6 = y - 2 9 = z 12 . Trong các mệnh đề sau, mệnh đề nào đúng khi nói về vị trí tương đối của hai đường thẳng trên?
A. Song song
B. Chéo nhau
C. Song song
D. Cắt nhau
Chọn B.
Đường thẳng d có VTCP ![]()
Đường thẳng d’ có VTCP ![]()
Từ đó ta có:
![]()
Lại có:
![]()
Suy ra d và d’ chéo nhau.
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d : x = 1 + t y = 2 + 3 t z = 3 - t , d ' : x = 2 - 2 t ' y = - 2 + t ' z = 1 + 3 t ' . Tìm tọa độ giao điểm M của hai đường thẳng d và d’
A. M(-1;0;4)
B. M(4;0;-1)
C. M(0;4;-1)
D. M(0;-1;4)
Trong không gian Oxyz, cho hai đường thẳng d : x = 1 + t y = 2 - t z = t , d ' : x = 2 t ' y = 1 + t ' z = 2 + t ' . Đường thẳng ∆ cắt d, d ' lần lượt tại các điểm A, B thỏa mãn độ dài đoạn thẳng AB nhỏ nhất. Phương trình đường thẳng ∆ là
A. x - 1 - 2 = y - 2 1 = z 3
B. x - 4 - 2 = y - 1 = z - 2 3
C. x 2 = y - 3 - 1 = z + 1 - 3
D. x - 2 - 2 = y - 1 1 = z - 1 3