Giá trị lớn nhất của hàm số y = x 2 + 16 x trên đoạn 1 3 ; 4 bằng
A. 433 9
B. 443 9
C. 344 9
D. 20
tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số trên đoạn [2;4]
y=\(\dfrac{x^2+3}{x-1}\)
Giá trị lớn nhất của hàm số y=x-1/x+2 trên đoạn [0;1] là:
\(y'=\dfrac{3}{\left(x+2\right)^2}>0\Rightarrow\) hàm đồng biến trên đoạn đã cho
\(\Rightarrow\max\limits_{\left[0;1\right]}y=y\left(1\right)=0\)
Tìm giá trị lớn nhất của hàm số y=e^x(x^2-x-5) trên đoạn [1;3].
A.![]()
B. ![]()
C. ![]()
D. ![]()
Giá trị lớn nhất của hàm số y = x + 4 x - 2 trên đoạn [3;4]
A. -4
B. 10
C. 7
D. 8
Cho hàm số y = − x 2 + 2 , khi x ≤ 1 x , k h i x > 1 . Tìm giá trị lớn nhất của hàm số trên đoạn − 2 ; 3
A. max − 2 ; 3 y = − 2
B. max − 2 ; 3 y = 2
C. max − 2 ; 3 y = 1
D. max − 2 ; 3 y = 3
Đáp án D
Với x ∈ − 2 ; 1 ta có
y = − x 2 + 2 ⇒ y ' = − 2 x ; y ' = 0 ⇔ x = 0.
Ta có y − 2 = − 2 ; y 0 = 2 ; y 1 = 1
Xét x ∈ 1 ; 3 ta có
y = x ⇒ y ' = 1 > 0.
Ta có y 3 = 3
Suy ra max − 2 ; 3 y = 3
Cho hàm số y=f(x) có bảng biến thiên như sau:
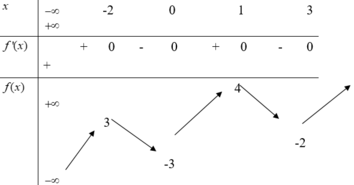
Tích của giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=f(x) trên đoạn [-2;3] bằng
A. -6
B. -8
C. -12
D. -9
Cho hàm số y=f(x) liên tục, không âm trên R thỏa mãn f ( x ) . f ' ( x ) = 2 x f ( x ) 2 + 1 và f(0)=0. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y=f(x) trên đoạn [1;3] lần lượt là:
A. M=20;m=2
B. M = 4 11 ; m = 3
C. M = 20 ; m = 2
D. M = 3 11 ; m = 3
Giá trị lớn nhất của hàm số y = x ( 2 - ln x ) trên đoạn [2;3] bằng
A.3
![]()
![]()
D.e
Giá trị lớn nhất của hàm số y = x − 1 x + 2 trên đoạn [0;2]là:
A. 1/4
B. 2
C. - 1/2
D. 0
Đáp án A
TXĐ: D = ℝ \ − 2 Ta có: y ' = 3 x + 2 2 > 0 ; ∀ x ∈ D
Khi đó: y 0 = − 1 2 ; y 2 = 1 4 ⇒ Hàm số có giá trị lớn nhất bằng 1/4
Giá trị lớn nhất của hàm số y = x + 1 x - 2 trên đoạn [3;5] là
A. - 1 2
B. 5
C. 4
D. 2
Đáp án D
Ta có: y’ = − 3 ( x − 2 ) 2
Dễ thấy hàm số nghịch biến trên (-∞;2) và (2;+∞)
ð Hàm có giá trị lớn nhất là 2 tại x = 5 trên đoạn [3;5]