Cho hình hộp chữ nhật ABCD.ABCD có Tính theo thể tích khối hợp đã cho.
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có 
Tính theo thể tích khối hợp đã cho.
Những câu hỏi liên quan
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
a
,
A
D
a
2
,
A
B
a
5
. Tính theo a thể tích khối hộp đã cho A.
V
a
3
10
B....
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = a , A D = a 2 , A B ' = a 5 . Tính theo a thể tích khối hộp đã cho
A. V = a 3 10
B. V = 2 a 3 2 3
C. V = a 3 2
D. V = 2 a 3 2
Đáp án D
S A B C D = a 2 Ta có B B ' = A B ' 2 − A B 2 = 2 a
⇒ V A B C D . A ' B ' C ' D ' = S A B C D . B B ' = 2 a 3 2 d v d t
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.ABCD có AD
2
a
. Tính theo a thể tích V của khối hộp ABCD.ABCD
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AD= 2 a . Tính theo a thể tích V của khối hộp ABCD.A'B'C'D'
Cho hình hộp chữ nhật ABCD.ABCD có
A
D
2
a
,
A
C
2
3
a
. Tính theo a thể tích V của khối hộp ABCD.ABCD A.
V
2
6
a
3
B.
V
2
6...
Đọc tiếp
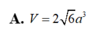
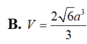
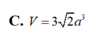
Cho hình hộp chữ nhật ABCD.A'B'C'D' có A D = 2 a , A C ' = 2 3 a . Tính theo a thể tích V của khối hộp ABCD.A'B'C'D'
A. V = 2 6 a 3
B. V = 2 6 a 3 3
C. V = 3 2 a 3
D. V = 6 a 3
Đáp án C
Ta có: A A ' = 2 3 a 2 − a 2 − 2 a 2 = 3 a
Thể tích khối hộp là: V = A A ' . S A B C D = 3 a . a 2 a = 3 2 a 3
Đúng 0
Bình luận (0)
Cho khối hộp chữ nhật ABCD.ABCD có thể tích là V. Biết AM MA, DN 3ND, CP 2PC. Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Tính thể tích khối đa diện nhỏ hơn tính theo V bằng? A.
5
V
12
B.
7
V
12
C.
V
4
D.
V
6
Đọc tiếp
Cho khối hộp chữ nhật ABCD.A'B'C'D' có thể tích là V. Biết A'M = MA, DN = 3ND', CP = 2PC'. Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Tính thể tích khối đa diện nhỏ hơn tính theo V bằng?
A. 5 V 12
B. 7 V 12
C. V 4
D. V 6
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = b, AA'=c. Gọi M và N theo thứ tự là trung điểm của A'B' và B'C'
Tính tỉ số giữa thể tích khối chóp D'DMN và thể tích khối hộp chữ nhật ABCD.A'B'C'D' ?
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
a
,
A
D
2
a
,
A
C
2
3
a
. Tính theo a thể tích V của khối hộp ABCD.A’B’C’D’. A.
V
2
6
a
3
B...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = a , A D = 2 a , A C ' = 2 3 a . Tính theo a thể tích V của khối hộp ABCD.A’B’C’D’.
A. V = 2 6 a 3
B. V = 2 6 3 a 3
C. V = 3 2 a 3
D. V = 6 a 3
Đáp án C
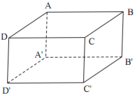
Phương pháp:
Thể tích khối hộp chữ nhật: V = abc
Cách giải:
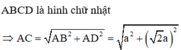
= 3 a
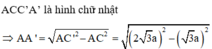
= 3a
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
a
,
A
D
a
3
và
C
C
2
a
. Khối trụ ngoại tiếp hình hộp chữ nhật đã cho có thể tích bằng A.
8
πa
3
B....
Đọc tiếp
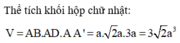
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = a , A D = a 3 và C C ' = 2 a . Khối trụ ngoại tiếp hình hộp chữ nhật đã cho có thể tích bằng
A. 8 πa 3
B. 2 3 πa 3
C. 2 πa 3
D. 4 πa 3
Chọn đáp án C.
Bán kính đáy của khối trụ ngoại tiếp hình hộp chữ nhật đã cho là
Đúng 0
Bình luận (0)
Cho khối hợp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
2
B
C
2
a
v
à
A
C
3
a
. Thể tích khối hộp đã cho bằng A.
6
a
3
B.
4...
Đọc tiếp
Cho khối hợp chữ nhật A B C D . A ' B ' C ' D ' có A B = 2 B ' C ' = 2 a v à A C ' = 3 a . Thể tích khối hộp đã cho bằng
A. 6 a 3
B. 4 3 a 3
C. 2 6 a 3
D. 4 a 3
Cho hình hộp chữ nhật ABCD.ABCD có diện tích các mặt ABCD, BCCB, CDDC lần lượt là 2a2, 3a2, 6a2. Tính thể tích khối hộp chữ nhật ABCD.ABCD. A. 36a3 B. 6a3 C. 36a6 D. 6a2
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có diện tích các mặt ABCD, BCC'B', CDD'C' lần lượt là 2a2, 3a2, 6a2. Tính thể tích khối hộp chữ nhật ABCD.A'B'C'D'.
A. 36a3
B. 6a3
C. 36a6
D. 6a2
Đáp án B
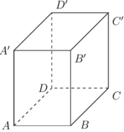
Ta đặt AB=x, AD=y, AA'=z. Khi đó theo giả thiết ta có:
x y = 2 a 2 x z = 3 a 2 y z = 6 a 2 ⇔ x y = 2 a 2 x z = 3 a 2 y z = 6 a 2 x y z = 6 a 3 ⇔ x = a y = 2 a z = 3 a
Vậy thể tích khối hôp chữ nhật V=6a3.
Đúng 0
Bình luận (0)