Cho hàm số y = a x 0 < a < 1  có đồ thị hàm số C . Mệnh đề nào sau đây là sai ?

A. Đồ thị (C) có tiệm cận y = 0

B. Đồ thị (C) luôn nằm phía trên trục hoành

C. Đồ thị (C) luôn đi qua M(0;1)

D. Hàm số luôn đồng biến trên  ℝ

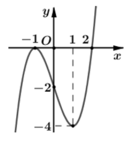
Cho hàm số y=f(x)= a x 4 + b x 3 + c x 2 + d x + e  , đồ thị hình bên là đồ thị của hàm số y=f'(x) . Xét hàm số g x = f ( x 2 + 2 ) . Mệnh đề nào dưới đây sai?

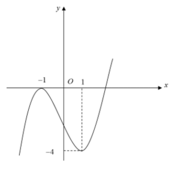
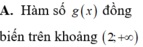
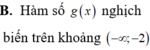
Cho hàm số  y= f(x) = ax⁴+ bx³+ cx²+ dx+ e, đồ thị hình bên là đồ thị của hàm số y= f’( x) . Xét hàm số g(x) = f( x²-2). Mệnh đề nào dưới đây sai?

A. Hàm số y= g(x)  nghịch biến trên khoảng

B. Hàm số y= g(x)  đồng biến trên khoảng 

C. Hàm số y= g(x)  nghịch biến trên khoảng ( -1; 0)

D. Hàm số y= g(x)  nghịch biến trên khoảng ( 0; 2)

Đồ thị hàm số y = a x + 4 3 x + b  đi qua điểm A 1 ; 9 10 ; B 1 2 ; 13 17  Hỏi mệnh đề nào sau đây là đúng ?

A. a + b = 11

B. a - b = 2

C. ab = 35

D.  a b = 1 2

Đồ thị hàm số y = a x 3 + b x 2 + c x + d  có đồ thị như hình vẽ sau (đồ thị không đi qua gốc tọa độ ). Mệnh đề nào sau đây đúng.

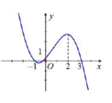
A. a < 0 ; b > 0 ; c > 0 ; d > 0.

B. a < 0 ; b > 0 ; c < 0 ; d > 0.

C. a < 0 ; b < 0 ; c < 0 ; d > 0.

D. a < 0 ; b < 0 ; c > 0 ; d > 0.

Cho hàm số y = f(x) là hàm số đa thức bậc bốn, có đồ thị hàm số y = f'(x) như hình vẽ

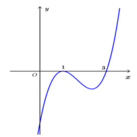
Mệnh đề nào sau đây là sai?

A. Hàm số y = f(x) đạt giá trị nhỏ nhất bằng f(3).

B. Hàm số y = f(x) nghịch biến trên khoảng  - ∞ ; 3  .

C. Hàm số y = f(x) đồng biến trên khoảng  - ∞ ; 1 .

D. Hàm số y = f(x) có một điểm cực trị.