Tìm mô đun của số phức z = 3 - 2 i
A. z = 13
B. z = 5
C. z = 13
D. z = 5
Những câu hỏi liên quan
Cho số phức z thỏa mãn
z
1
-
3
i
3
1
-
i
. Tìm mô đun của số phức
z
+
i
z
A. 8 B. -8 C.
8
2
D. 16
Đọc tiếp
Cho số phức z thỏa mãn z = 1 - 3 i 3 1 - i . Tìm mô đun của số phức z + i z
A. 8
B. -8
C. 8 2
D. 16
Ta có
z = 1 - 3 i 3 1 - i = - 4 - 4 i ⇒ z = - 4 - 4 i ⇒ z + i z = - 8 - 8 i
Vậy z + i z = 8 2 + 8 2 = 8 2
Đáp án C
Đúng 0
Bình luận (0)
Trong các số phức z thỏa mãn |z - 3i| + | i z ¯ + 3| =10 , tìm số phức z có mô-đun nhỏ nhất.
A. z = 2 hoặc – 2
B. z= 3 hoặc – 3
C. z = 4 hoặc – 4
D. tất cả sai
Chọn C.
Áp dụng công thức: 
Ta có: 
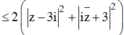
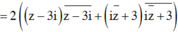
Giải bất phương trình 100 ≤ 4 ta có 
ta có 0 ≤ |z| ≤ 4
Vậy min|z| = 4 đạt được khi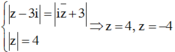 
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
(
2
+
3
i
)
z
-
(
1
+
2
i
)
z
¯
7
-
i
. Tìm mô đun của z. A.
z
1 B.
z...
Đọc tiếp
Cho số phức z thỏa mãn ( 2 + 3 i ) z - ( 1 + 2 i ) z ¯ = 7 - i . Tìm mô đun của z.
A. z =1
B. z =2
C. z = 3
D. z = 5
Đáp án D
Phương pháp:
Đặt z=a+bi, giải phương trình để tìm a, b
Cách giải: 
Đúng 0
Bình luận (0)
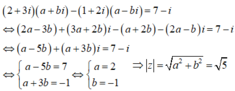
Cho số phức z thỏa mãn (2+3i)z - (1+2i) z = 7 - i. Tìm mô đun của z
A. |z| = 1
B. |z| = 2
C. |z| = 3
D. |z| = 5
Cho số phức z thỏa mãn
z
+
i
+
1
z
¯
−
2
i
. Tìm giá trị nhỏ nhất của mô đun của số phức z. A.
1
2
B.
2
C.
1...
Đọc tiếp
Cho số phức z thỏa mãn z + i + 1 = z ¯ − 2 i . Tìm giá trị nhỏ nhất của mô đun của số phức z.
A. 1 2
B. 2
C. 1 2
D. 1 4
Cho số phức z thỏa mãn |z+i+1||
z
-2i|. Tìm giá trị nhỏ nhất của mô đun của số phức z. A.
1
2
B.
1
2
C.
2
D.
1
4
Đọc tiếp
Cho số phức z thỏa mãn |z+i+1|=| z -2i|. Tìm giá trị nhỏ nhất của mô đun của số phức z.
A. 1 2
B. 1 2
C. 2
D. 1 4
Số phức thỏa mãn phương trình
z
+
3
z
¯
(
2
+
i
)
3
(
2
-
i
)
Mô đun của số phức
w
z
+
10
i
là
Đọc tiếp
Số phức thỏa mãn phương trình z + 3 z ¯ = ( 2 + i ) 3 ( 2 - i ) Mô đun của số phức w = z + 10 i là
Tìm mô đun của số phức z biết
2
z
-
1
1
+
i
+
z
¯
‐
1
1
-
i
2
-
2
i
. A....
Đọc tiếp
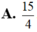
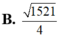
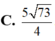
Tìm mô đun của số phức z biết 2 z - 1 1 + i + z ¯ ‐ 1 1 - i = 2 - 2 i .
A. 1 9
B. 2 3
C. 2 9
D. 1 3
Tìm số phức z có mô đun nhỏ nhất thỏa mãn
i
z
-
3
z
-
2
-
i
A.
z
-
1
5
-
2
5
i
B.
z
-
1
5
+...
Đọc tiếp
Tìm số phức z có mô đun nhỏ nhất thỏa mãn i z - 3 = z - 2 - i
A. z = - 1 5 - 2 5 i
B. z = - 1 5 + 2 5 i
C. z = 1 5 - 2 5 i
D. z = 1 5 + 2 5 i
Giả sử z = a + bi với a , b ∈ R
Khi đó
i z - 3 = z - 2 - i = b + 3 2 + a 2 = a - 2 2 + b - 1 2 ⇔ a = - 2 b - 1
Suy ra
z = a 2 + b 2 = - 2 b - 1 2 + b 2 = 5 b 2 + 4 b + 1 = 9 b + 2 5 2 + 1 5 ≥ 5 5
Dấu “=” xảy ra khi và chỉ khi a = - 1 5 ; b = - 2 5
Vậy số phức z cần tìm là z = - 1 5 - 2 5 i
Đáp án A
Đúng 0
Bình luận (0)
Trong các số phức z thỏa mãn | z - 2 + i | = | z ¯ + 1 -4i | , tìm số phức có mô-đun nhỏ nhất.
A. z = 1
B. z = 1 - i
C. z = -1 - i
D. z = 2 - i
Chọn C.
Giả sử z = a+ bi. Khi đó:
z – 2 + i = ( a - 2) + ( b + 1) i và 
Vậy z = -1 - i thỏa mãn đề bài.
Đúng 0
Bình luận (0)