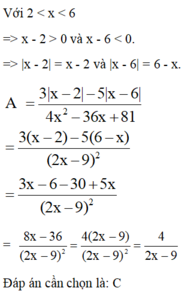Rút gọn phân thức sau: x 3 - 5 x 2 + 6 x - 4 x 2 + 10 x - 4

Những câu hỏi liên quan
5.phân thức 4x/3 bằng với phân thức nào sau đây? A. -8x/6 b. 8x/6 c. 7x/6 D. 6/8x 6. Tìm điều kiện xác định của các phân thức sau A) x^2-1/x-2 b) 2x^2+3/x+1 7. Rút gọn các phân thức sau: A) 8x^3yz/24xy^2 b) 12x^4y^2z/x+1 8.thực hiện các phép tính sau: A) x^2+4/3x^2-6x + 5x+2/3x -4x/3x^2-6x
Câu 5: B
Câu 6:
a: ĐKXĐ: \(x-2\ne0\)
=>\(x\ne2\)
b: ĐKXĐ: \(x+1\ne0\)
=>\(x\ne-1\)
8:
\(A=\dfrac{x^2+4}{3x^2-6x}+\dfrac{5x+2}{3x}-\dfrac{4x}{3x^2-6x}\)
\(=\dfrac{x^2+4-4x}{3x\left(x-2\right)}+\dfrac{5x+2}{3x}\)
\(=\dfrac{\left(x-2\right)^2}{3x\left(x-2\right)}+\dfrac{5x+2}{3x}\)
\(=\dfrac{x-2+5x+2}{3x}=\dfrac{6x}{3x}=2\)
7:
\(\dfrac{8x^3yz}{24xy^2}\)
\(=\dfrac{8xy\cdot x^2z}{8xy\cdot3y}\)
\(=\dfrac{x^2z}{3y}\)
Đúng 2
Bình luận (0)
rút gọn phân thức sau:
x^7+x^6+x^5+x^4+x^3+x^2
x^2-1
Rút gọn phân thức A
3|x
−
2|
−
5|x
−
6|
4x
2
−
36x
+
81
với 2 x 6 ta được? A.
A
4
x
−
9...
Đọc tiếp
Rút gọn phân thức A = 3|x − 2| − 5|x − 6| 4x 2 − 36x + 81 với 2 < x < 6 ta được?
A. A = 4 x − 9
B. A = 4 9 − 2x
C. A = 4 2x − 9
D. A = 8 2x − 9
\(^{\dfrac{x+2}{x+3}-\dfrac{5}{x^2+x-6}+\dfrac{1}{2-x}}\)
a,rút gọn phân thức
\(ĐKXĐ:\left\{{}\begin{matrix}x\ne-3\\x\ne2\end{matrix}\right.\)
\(\dfrac{x+2}{x+3}-\dfrac{5}{x^2+x-6}+\dfrac{1}{2-x}\)
\(=\dfrac{x^2-4-5-\left(x+3\right)}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x^2-x-12}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{\left(x-4\right)\left(x+3\right)}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x-4}{x-2}\)
Đúng 0
Bình luận (4)
Làm chi tiết theo yêu cầu của bạn :
\(ĐKXĐ\left\{{}\begin{matrix}x\ne-3\\x\ne2\end{matrix}\right.\)
\(\dfrac{x+2}{x+3}-\dfrac{5}{x^2+x-6}+\dfrac{1}{2-x}\)
\(=\dfrac{x+2}{x+3}-\dfrac{5}{\left(x+3\right)\left(x-2\right)}-\dfrac{1}{x-2}\)
\(=\dfrac{\left(x+2\right)\left(x-2\right)-5-\left(x+3\right)}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x^2-4-5-x-3}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x^2-x-12}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{\left(x-4\right)\left(x+3\right)}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x-4}{x-2}\)
p/s : bonus nếu bạn không hiểu ptich đa thức thành nhân tử =))
x2 + x - 6 = x2 + 3x - 2x - 6 = x(x+3) - 2(x+3) = (x-2)(x+3)
x2 - x - 12 = x2 + 3x - 4x - 12 = x(x+3) - 4(x+3) = (x-4)(x+3)
Đúng 0
Bình luận (3)
Bài 5 : rút gọn biểu thức sau
2x^3(x^2 - 5)+(-2x^3 +4x)+(6+x)x^2
Xem chi tiết
\(2x^3\left(x^2-5\right)+\left(-2x^3+4x\right)+\left(6+x\right)x^2\)
\(=2x^5-10x^3-2x^3+4x+6x^2+x^3=2x^5-9x^3+6x^2+4x\)
Rút gọn phân thức sau: a) (3x-6)/(x^3-6x^2+12x-8) b) (x^3+2x^2)/(x^3+6x^2+12x+8)
a: \(=\dfrac{3\left(x-2\right)}{\left(x-2\right)^3}=\dfrac{3}{\left(x-2\right)^2}\)
b: \(=\dfrac{x^2\left(x+2\right)}{\left(x+2\right)^3}=\dfrac{x^2}{\left(x+2\right)^2}\)
Đúng 2
Bình luận (1)
Rút gọn phân thức sau : (x - 2) (3/x+2 - 5/2x-4 + 8/x^2 - 4)
a kham khảo nha , e nhờ a e lm chứ ko phải e lm nha !
\(\left(x-2\right)\left(\frac{3}{x}+2-\frac{5}{2x}-4+\frac{8}{x^2}-4\right)\)
\(\left(x-2\right)\left[\left(\frac{3}{x}-\frac{5}{2x}\right)-6+\frac{8}{x^2}\right]\)
\(\left(x-2\right)\left(\frac{1}{2x}-6+\frac{8}{x^2}\right)\)
\(\left(x-2\right)\left(\frac{3}{x+2}-\frac{5}{2x-4}+\frac{8}{x^2-4}\right)\)
\(=\left(x-2\right)\left[\frac{3}{x+2}-\frac{5}{2\left(x-2\right)}+\frac{8}{\left(x-2\right)\left(x+2\right)}\right]\)
\(=\left(x-2\right)\left[\frac{3.2\left(x-2\right)}{2\left(x-2\right)\left(x+2\right)}-\frac{5\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)}+\frac{8.2}{2\left(x-2\right)\left(x+2\right)}\right]\)
\(=\left(x-2\right)\left[\frac{6\left(x-2\right)}{2\left(x-2\right)\left(x+2\right)}-\frac{5\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)}+\frac{16}{2\left(x-2\right)\left(x+2\right)}\right]\)
\(=\left(x-2\right)\left[\frac{6\left(x-2\right)-5\left(x+2\right)+16}{2\left(x-2\right)\left(x+2\right)}\right]\)
\(=\frac{\left(x-2\right)\left(x-6\right)}{2\left(x-2\right)\left(x+2\right)}\)
\(=\frac{x-6}{2\left(x+2\right)}\)
rút gọn phân thức sau
\(\dfrac{x^6+2x^3y^3+y^6}{x^7-xy^6}\)
Ta có: \(\dfrac{x^6+2x^3y^3+y^6}{x^7-xy^6}\)
\(=\dfrac{\left(x^3+y^3\right)^2}{x\left(x^6-y^6\right)}\)
\(=\dfrac{\left(x^3+y^3\right)\left(x^3+y^3\right)}{x\left(x^3+y^3\right)\left(x^3-y^3\right)}\)
\(=\dfrac{x^3+y^3}{x\left(x^3-y^3\right)}\)
\(=\dfrac{\left(x+y\right)\left(x^2-xy+y^2\right)}{x\left(x-y\right)\left(x^2+xy+y^2\right)}\)
Đúng 1
Bình luận (0)
\(\dfrac{x^6+2x^3y^3+y^6}{x^7-xy^6}=\dfrac{\left(x^3+y^3\right)^2}{x\left(x^6-y^6\right)}=\dfrac{\left(x^3+y^3\right)^2}{x\left(x^3-y^3\right)\left(x^3+y^3\right)}=\dfrac{x^3+y^3}{x\left(x^3-y^3\right)}=\dfrac{\left(x+y\right)\left(x^2-xy+y^2\right)}{\left(x^2-y^2\right)\left(x^2+y^2\right)}=\dfrac{\left(x+y\right)\left(x^2-xy+y^2\right)}{\left(x-y\right)\left(x+y\right)\left(x^2+y^2\right)}=\dfrac{x^2-xy+y^2}{x^3+xy^2-x^2y-y^3}\)
Đúng 0
Bình luận (1)
Rút gọn biểu thức sau:
(√12 - 2√18 + 5√3) x √3+5√6
Ta có: \(\left(\sqrt{12}-2\sqrt{18}+5\sqrt{3}\right)\cdot\sqrt{3}+5\sqrt{6}\)
\(=\left(2\sqrt{3}-6\sqrt{3}+5\sqrt{3}\right)\cdot\sqrt{3}+5\sqrt{6}\)
\(=3+5\sqrt{6}\)
Đúng 2
Bình luận (0)
Rút gọn phân thức sau ( phân thức đều có nghĩa )
\(N=\dfrac{\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)+1}{x^2+7x+11}\)
\(N=\dfrac{\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)+1}{x^2+7x+11}\)
\(=\dfrac{\left[\left(x+2\right)\left(x+5\right)\right]\cdot\left[\left(x+3\right)\left(x+4\right)\right]+1}{x^2+7x+11}\)
\(=\dfrac{\left(x^2+7x+10\right)\left(x^2+7x+12\right)+1}{x^2+7x+11}\)
Đặt \(x^2+7x+11=y\), thay vào \(N\) ta được:
\(N=\dfrac{\left(y-1\right)\left(y+1\right)+1}{y}\)
\(=\dfrac{y^2-1+1}{y}\)
\(=\dfrac{y^2}{y}\)
\(=y\)
\(=x^2+7x+11\)
Vậy \(N=x^2+7x+11\).
\(\text{#}Toru\)
Đúng 5
Bình luận (8)