Tọa độ tất cả các điểm thuộc đồ thị (C) của hàm số y = x + 1 x - 2 sao cho tổng khoảng cách từ điểm đó đến 2 tiệm cận là nhỏ nhất là
A. (1;1)
B.![]()
C. ![]()
D. ![]()
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = - x - 1 3 + 3 m x - 1 - 2 có hai điểm cực trị cách đều gốc tọa độ. Tổng các giá trị tuyệt đối của tất cả các phần tử thuộc S là
A. 4.
B. 2 3
C. 1.
D. 5.

![]()
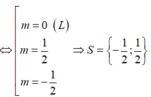
Vậy tổng các giá trị tuyệt đối của tất cả các phần tử thuộc S là 1.
Chọn C
Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị hàm số y = - x - 1 3 + 3 m 2 x - 1 - 2 có hai điểm cực trị cách đều gốc tọa độ. Tổng các giá trị tuyệt đối của tất cả các phần tử thuộc S là
A. 4.
B. 2/3
C. 1.
D. 5.
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 m x 2 + 3 ( m 2 - 1 ) x - m 3 + m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O
A. m = - 3 - 2 2 h o ặ c m = - 1
B. m = - 3 + 2 2 h o ặ c m = - 1
C. m = - 3 + 2 2 h o ặ c m = - 3 - 2 2 .
D. m = - 3 + 2 2
Chọn C
Ta có y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 )
Hàm số (1) có cực trị thì PT y ' = 0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nhiệm phân biệt
![]()
Khi đó, điểm cực đại A ( m - 1 ; 2 - 2 m ) và điểm cực tiểu B ( m + 1 ; - 2 m )
Ta có O A = 2 O B ⇔ m 2 + 6 m + 1 = 0
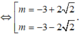
Trong tất cả các điểm có tọa độ nguyên thuộc đồ thị (C) của hàm số 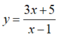 , số điểm có hoành độ lớn hơn tung độ là
, số điểm có hoành độ lớn hơn tung độ là
A.2
B.8
C.6
D.4
Cho hàm số y=x2
1. Cho các hàm số y = x + 2 và y=-x + m ( với m là tham số) lần lượt có đồ thị là (d) và (d1). Tìm tất cả các giá trị của m để trên 1 mặt phẳng tọa độ các đồ thị của (P),(d) (d1) cùng đi qua một điểm
G/s (P),(d),(d1) cùng đi qua một điểm
Gọi I(a,b) là giao điểm của (P),(d),(d1)
Có \(I\in\left(P\right),\left(d\right),\left(d1\right)\)\(\Rightarrow\left\{{}\begin{matrix}b=a^2\left(1\right)\\b=a+2\left(2\right)\\b=-a+m\left(3\right)\end{matrix}\right.\)
Từ (1);(2)\(\Rightarrow a^2=a+2\)
\(\Leftrightarrow\left[{}\begin{matrix}a=2\\a=-1\end{matrix}\right.\)
TH1: Tại \(a=2\Rightarrow b=a^2=4\)
Thay \(a=2;b=4\) vào (3) ta được:\(4=-2+m\) \(\Leftrightarrow m=6\)
TH2: Tại \(a=-1\Rightarrow b=a^2=1\)
Thay \(a=-1;b=1\) vào (3) ta được:\(1=1+m\) \(\Leftrightarrow m=0\)
Vậy m=6 hoặc m=0
Phương trình hoành độ giao điểm của (d) và (P):
\(x^2=x+2\)
\(\Leftrightarrow x^2-x-2=0\)(*)
Ta có: \(a-b+c=1-\left(-1\right)+\left(-2\right)=0\)
Do đó phương trình (*) có 2 nghiệm phân biệt
\(x_1=-1;x_2=\dfrac{-c}{a}=2\)
\(x_1=-1\) thì \(y_1=x_1^2=\left(-1\right)^2=1\)
\(x_2=2\) thì \(y_2=x_2^2=2^2=4\)
Vậy (d) và (P) cắt nhau tại 2 điểm phân biệt \(A\left(-1;1\right);B\left(2;4\right)\)
Do đó các đồ thị của (P), (d) và \(\left(d_1\right)\)cùng đi qua 1 điểm
\(\Leftrightarrow\left[{}\begin{matrix}A\in\left(d_1\right)\\B\in\left(d_1\right)\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}1=1+m\\4=-2+m\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=6\end{matrix}\right.\)
Vậy khi m=0 hoặc m=6 thì các đồ thị của (P),(d) và cùng đi qua 1 điểm
-Chúc bạn học tốt-
Tính tổng tất cả các giá trị thực của tham số m để hàm số y= x3-3mx2+ 3( m2-1) x- m3+ m có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số đến gốc tọa độ O bằng 2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến gốc tọa độ O.
A. -4
B. -5
C. -6.
D. -7
Ta có y’ = 3x2- 6mx + 3( m2-1).
Hàm số đã cho có cực trị thì phương trình y’ =0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nghiệm phân biệt ⇔ ∆ = 1 > 0 , ∀ m
Khi đó, điểm cực đại A( m-1; 2-2m) và điểm cực tiểu B( m+1; -2-2m)
Ta có
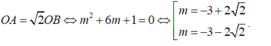
Tổng hai giá trị này là -6.
Chọn C.
Cho hàm số (d): y=2x+3. a, Vẽ đồ thị của hàm số đã cho. b, Tìm tọa độ giao điểm của (d) với hai trục tọa độ. c) Trong các điểm sau, điểm nào thuộc đồ thị hàm số, điểm nào không thuộc đồ thị hàm số: A( -1; 1) B( 2; 3) C(1/2;4)
Cho hàm số y = x 3 − 6 x 2 + 9 x − 1 có đồ thị là (C). Gọi T là tập hợp tất cả các điểm thuộc đường thẳng y=x-1 mà từ điểm đó kẻ được đúng 2 tiếp tuyến đến đồ thị (C). Tìm tổng tung độ của các điểm thuộc T.
A. ‒1
B. 0
C. 1
D. 2
Cho hàm số y = x 3 − 6 x 2 + 9 x − 1 có đồ thị là (C). Gọi T là tập hợp tất cả các điểm thuộc đường thẳng y = x − 1 mà từ điểm đó kẻ được đúng 2 tiếp tuyến đến đồ thị (C). Tìm tổng tung độ của các điểm thuộc T
A. ‒1
B. 0
C. 1
D. 2
Đáp án D.
y ' = 3 x 2 − 12 x + 9
Gọi M x 0 ; x 0 3 − 6 x 0 2 + 9 x 0 − 1 là một điểm bất kì thuộc (C) . Tiếp tuyến tại M:
y = 3 x 0 2 − 12 x 0 + 9 x − x 0 + x 0 3 − 6 x 0 2 + 9 x 0 − 1
⇔ y = 3 x 0 2 − 12 x 0 + 9 x − 2 x 0 3 + 6 x 0 2 − 1
Gọi A a ; a − 1 là một điểm bất kì thuộc đường thẳng y = x − 1 .
Tiếp tuyến tại M đi qua A ⇔ 3 x 0 2 − 12 x 0 + 9 a − 2 x 0 3 + 6 x 0 2 − 1 = a − 1
⇔
3
x
0
2
−
12
x
0
+
8
a
=
2
x
0
3
−
6
x
0
2
(*).
Từ A kẻ được hai tiếp tuyến đến C ⇔ * có hai nghiệm phân biệt.
Ta có
3 x 0 2 − 12 x 0 + 8 = 0 ⇔ x 0 = 6 ± 2 3 3
Dễ thấy x 0 = 6 ± 2 3 3 không thỏa mãn .
Với x 0 ≠ 6 ± 2 3 3 thì * ⇔ a = 2 x 0 3 − 6 x 0 2 3 x 0 2 − 12 x 0 + 8 .
Xét hàm số f x = 2 x 3 − 6 x 2 3 x 2 − 12 x + 8 . Ta có f ' x = 6 x 4 − 8 x 3 + 20 x 2 − 16 x 3 x 2 − 12 x + 8 2 .
Bảng biến thiên của :
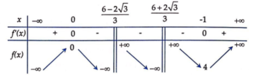
Vậy để (*) có 2 nghiệm phân biệt thì a ∈ 0 ; 4 . Suy ra tập T = 0 ; − 1 , 4 ; 3
Do đó tổng tung độ các điểm thuộc T bằng 2.