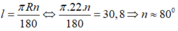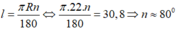Một đường tròn có bán kính 25 cm. Tìm độ dài của các cung trên đường tròn có số đo 4 / 3

Những câu hỏi liên quan
Một đường tròn có bán kính 25 cm. Tìm độ dài của các cung trên đường tròn có số đo 49 ο
Một đường tròn có bán kính 25 cm. Tìm độ dài của các cung trên đường tròn có số đo 3π / 7
Một đường tròn có bán kính 20cm. Tìm độ dài các cung trên đường tròn, có số đo
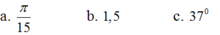
Từ công thức l = Rα (α có đơn vị là rad) ta có:
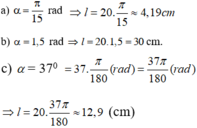
Đúng 0
Bình luận (0)
Một đường tròn có bán kính 25 cm. Tìm độ dài của các cung trên đường tròn đó có số đo :
a) \(\dfrac{3\pi}{7}\)
b) \(49^0\)
c) \(\dfrac{4}{3}\)
Áp dụng công thức: \(l=R\alpha\).
a) \(l=25.\dfrac{3\pi}{7}=\dfrac{75\pi}{7}\) (cm).
b) Đổi \(49^o=\dfrac{49\pi}{180}\).
\(l=25.\dfrac{49\pi}{180}\left(cm\right)=\dfrac{245}{36}cm\).
c) \(l=25.\dfrac{4}{3}\left(cm\right)=\dfrac{100}{3}cm\).
Đúng 0
Bình luận (0)
Một đường tròn có bán kính R 5(cm). Độ dài của cung trên đường tròn có số đo 135
°
là: A.
3
π
4
B.
5
π
4
C.
15
π
4
D.
15
π
2
Đọc tiếp
Một đường tròn có bán kính R = 5(cm). Độ dài của cung trên đường tròn có số đo 135 ° là:
A. 3 π 4
B. 5 π 4
C. 15 π 4
D. 15 π 2
Đáp án: C
Độ dài của cung trên đường tròn có số đo 135
°
là: 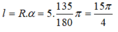
Đúng 0
Bình luận (0)
Một đường tròn có bán kính 20 cm. Tính độ dài của các cung trên đường tròn đó có số đo sau:
a) \(\frac{\pi }{{12}}\);
b) \(1,5\);
c) \({35^0}\);
d) \({315^0}\).
a) \(l = R\alpha = 20.\frac{\pi }{{12}} = \frac{{5\pi }}{3}\)
b) \(l = R\alpha = 20.1,5\pi = 30\pi \)
c) Đổi \({35^0} = 35.\frac{\pi }{{180}} = \frac{7\pi }{36}\)
\(l = R\alpha = 20.\frac{7\pi }{36} = \frac{35\pi }{9}\)
d) Đổi \({315^0} = 315.\frac{\pi }{{180}} = \frac{{7\pi }}{4}\)
\(l = R\alpha = 20.\left( {\frac{{7\pi }}{4}} \right) = 35\pi \)
Đúng 0
Bình luận (0)
Một đường tròn có bán kính 20 cm. Hỏi độ dài của cung trên đường tròn đó có số đo π/15 gần với giá trị nào nhất.
A. 4,1
B. 4,2
C. 4,3
D. 4,4
Chọn B.
Độ dài của cung 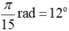 trên đường tròn được tính bằng công thức:
trên đường tròn được tính bằng công thức:
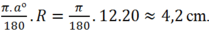
Đúng 0
Bình luận (0)
Số đo
n
°
của cung tròn có độ dài 30,8 cm trên đường tròn có bán kính 22 cm là (lấy
π
≃
3
,
14
và làm tròn đên độ) A.
70
°
B.
80
°
C.
65
°
D.
85
°
Đọc tiếp
Số đo n ° của cung tròn có độ dài 30,8 cm trên đường tròn có bán kính 22 cm là (lấy π ≃ 3 , 14 và làm tròn đên độ)
A. 70 °
B. 80 °
C. 65 °
D. 85 °
Số đo
n
°
của cung tròn có độ dài 30,8 cm trên đường tròn có bán kính 22 cm là (lấy
π
≃
3
,
14
và làm tròn đên độ) A.
70
°
B.
80
°
C.
65
°
D.
85
°
Đọc tiếp
Số đo n ° của cung tròn có độ dài 30,8 cm trên đường tròn có bán kính 22 cm là (lấy π ≃ 3 , 14 và làm tròn đên độ)
A. 70 °
B. 80 °
C. 65 °
D. 85 °