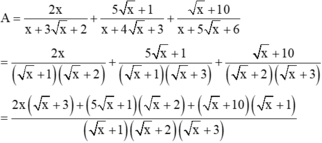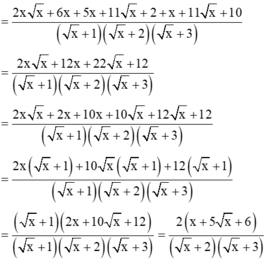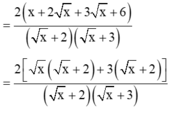-6x(1-X)+5x(2-5xX)=42

Những câu hỏi liên quan
Phân tích đa thức thành nhân tử:
1, x^3-x+y^3-4
2, 4x^2-y^2+4x+1
3, x^4+2x^3+x^2
4, x^2+5x-6
5, 7x-6x^2-2
6, 5x^2+5xy-x-y
7, 2x^2+3x-5
8,x^4-5x^2+4
9, x^3-5x^2+45-9x
10, x^4-2x^3-2x^2-2x-3
11, 81x^4+4
12,x^5+x+1
13, x^4+6x^3+7x^2-6x+1
14, x(x+4)(x+6)(x+10)+128
2: =(2x+1)^2-y^2
=(2x+1+y)(2x+1-y)
3: =x^2(x^2+2x+1)
=x^2(x+1)^2
4: =x^2+6x-x-6
=(x+6)(x-1)
5: =-6x^2+3x+4x-2
=-3x(2x-1)+2(2x-1)
=(2x-1)(-3x+2)
6: =5x(x+y)-(x+y)
=(x+y)(5x-1)
7: =2x^2+5x-2x-5
=(2x+5)(x-1)
8: =(x^2-1)*(x^2-4)
=(x-1)(x+1)(x-2)(x+2)
9: =x^2(x-5)-9(x-5)
=(x-5)(x-3)(x+3)
Đúng 1
Bình luận (0)
Cho biểu thức:
A=(6x−x2x+1+10x2−1).x+12−5xx−1(6x−x2x+1+10x2−1).x+12−5xx−1
a)Rút gọn A
b)chứng minh:với mọi x=±±1 thì A luôn có giá trị âm
c)tìm GTLN của A
a)A=1(6x-x2x+1+10x2-1)x-1(6x-x2x+1+10x2-1)x+12-5xx-5xx+12-1
A=\(14-10x^2-1\)
b)thay 1 vao A ta có
\(A=14-10.1^2-1=14-10-1=13\)
thay -1 vào A ta có
\(A=14-10\left(-1\right)^2-1=14+10-1=23\)
vậy với x=+-1 thì x luôn dương
c)
Đúng 0
Bình luận (0)
Cho
A
2
x
x
+
3
x
+
2
+
5
x
x
+
4
x
+
3
+
x
+
10...
Đọc tiếp
Cho A = 2 x x + 3 x + 2 + 5 x x + 4 x + 3 + x + 10 x + 5 x + 6 với x ≥ 0. Chọn đáp án đúng.
A. A = 2 x
B. Giá trị của A không phụ thuộc vào biến x
C. A = 3 x + 2
D. A = 2 x + 1
Mọi ng lm hộ mih nhé, giải pt:
1) \(\dfrac{5x-150}{50}+\dfrac{5x-102}{49}+\dfrac{5x-56}{48}+\dfrac{5x-12}{47}+\dfrac{5x-60}{46}=0\)
2) (x2 + 11x + 12)(x2 + 9x + 20)(x2 + 13x + 42) = 36(x2 + 11x + 30)(x2 + 11x + 31)
3) 6x4 - 11x3 + 3x2 + 11x - 6x2 + 3 = 0
tính ( 3x^3 - 5x^2 + 5x -2 ) : ( x^2 -x +1)
b) \(\frac{x+1}{x-3}\)-\(\frac{x-1}{x+3}\)+\(\frac{6x-42}{x^2-49}\)
a,
\(3x^3-5x^2+5x-2=3x^2-2x^2-3x^2+2x+3x-2=\left(x^2-x+1\right)\left(3x-2\right)\)
Ta có
\(\frac{3x^3-5x^2+5x-2}{x^2-x+1}=\frac{\left(3x-2\right)\left(x^2-x+1\right)}{x^2-x+1}=3x-2\)
Đúng 0
Bình luận (0)
tim x
5x-3{4x--22[4x-3(5xx-2)]}
nhanh minh tick
Xem thêm câu trả lời
điền vào chỗ trống:
(x-2).(6x^2-5x+1)
=x.6x^2+x.(-5x)+x.1+(-2).6x^2+(-2)(-5x)+(-2).1
=6x^3-5x^2+.....-12x^2+......-2
=6x^3-.......11x-2
....1x ...+10x
= -17x^2.......
Mình viết những cái cần điền
Nhớ đánh dấu cho mình nha
My Friend!
Đúng 0
Bình luận (0)
phân tích đa thức
x^4+6x^3+11x^2+6x+1
x^4+x^3+x^2+x+1
6x^4+5x^3-38x^2+5x+6
x^4+5x^3-12x^2+5x+1
a)\(x^4+6x^3+11x^2+6x+1\)
\(=x^4+9x^2+1+6x^3+6x+2x^2\)
\(=\left(x^2+3x+1\right)^2\)
Đúng 0
Bình luận (0)
\(x^4+5x^3-12x^2+5x+1\)
\(=\left(x^4-2x^3+x^2\right)+\left(7x^3-14x^2+7x\right)+\left(x^2-2x+1\right)\)
\(=x^2\left(x^2-2x+1\right)+7x\left(x^2-2x+1\right)+\left(x^2-2x+1\right)\)
\(=\left(x^2+7x+1\right)\left(x^2-2x+1\right)\)
\(=\left(x^2+7x+1\right)\left(x-1\right)^2\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
rút gọn biểu thức
(6x +1) ^2 +(6x-1)^2-2(1+6x)(6x-1)
x(2x^2-3)-x^2(5x+1)+x^2
3x(x-2)-5x(1-x)-8(x^2-3)
\(\left(6x+1\right)^2+\left(6x-1\right)^2-2\left(1+6x\right)\left(6x-1\right)\)
\(=\left(6x+1\right)^2-2\left(6x+1\right)\left(6x-1\right)+\left(6x-1\right)^2\)
\(=\left(6x+1-6x+1\right)^2\)
\(=4\)
\(x\left(2x^2-3\right)-x^2\left(5x+1\right)+x^2\)
\(=2x^3-3x-5x^3-x^2+x^2\)
\(=\left(2x^3-5x^3\right)+\left(x^2-x^2\right)-3x\)
\(=-3x^3-3x\)
\(3x\left(x-2\right)-5x\left(1-x\right)-8\left(x^2-3\right)\)
\(=3x^2-6x-5x+5x^2-8x^2+24\)
\(=\left(3x^2+5x^2-8x^2\right)-\left(6x+5x\right)+24\)
\(=-11x+24\)