Hệ thức liên hệ giữa độ tụ D và tiêu cự f của thấu kính là
A. D ( d p ) = 1 f ( m ) .
B. D ( d p ) = 1 - f ( m ) .
C. D ( d p ) = 1 f ( c m ) .
D. D ( d p ) = 1 f ( m ) .
Những câu hỏi liên quan
Hệ thức liên hệ giữa độ tụ D và tiêu cự f của thấu kính là A.
D
dp
1
f
m
B.
D
dp
1
−
f
m
C.
D
dp...
Đọc tiếp
Hệ thức liên hệ giữa độ tụ D và tiêu cự f của thấu kính là
A. D dp = 1 f m
B. D dp = 1 − f m
C. D dp = 1 f cm
D. D dp = 1 f m
Đáp án D
Theo công thức tính độ tụ D = 1 f . Về đơn vị thì D có đơn vị điốp (dp) thì tiêu cự phải lấy đơn vị mét (m)
Đúng 0
Bình luận (0)
Hệ thức liên hệ giữa độ tụ D và tiêu cự f của thấu kính là A.
D
d
p
1
f
m
B.
D
d
p
1
−
f
m...
Đọc tiếp
Hệ thức liên hệ giữa độ tụ D và tiêu cự f của thấu kính là
A. D d p = 1 f m
B. D d p = 1 − f m
C. D d p = 1 f c m
D. D d p = 1 f m
Chọn đáp án D.
Theo công thức tính độ tụ D = 1 f . Về đơn vị thì D có đơn vị điốp (dp) thì tiêu cự phải lấy đơn vị mét (m).
Đúng 0
Bình luận (0)
Hệ thức liên hệ giữa độ tụ D và tiêu cự f của thấu kính là A.
D
d
p
1
f
m
B.
D
d
p
1
-
f
m
C.
D
d...
Đọc tiếp
Hệ thức liên hệ giữa độ tụ D và tiêu cự f của thấu kính là
A. D d p = 1 f m
B. D d p = 1 - f m
C. D d p = 1 f c m
D. D d p = 1 f m
30 tháng 1 2022 lúc 16:52
Đố: Đặt vật sáng AB có độ cao h, vuông góc với trục chính của TKHT có tiêu cự f, điểm A nằm trên trục chính, cách thấu kính một khoảng d. Ảnh AB của vật AB có độ cao h và hứng được trên màn cách thấu kính khoảng d.a) Chứng minh rằng độ phóng đại ảnh kfrac{AB}{AB}frac{h}{h}frac{d}{d}b) Chứng minh mối liên hệ giữa tiêu cự của thấu kính, khoảng các từ vật đến thấu kính và khoảng cách từ ảnh đến thấu kính tuân theo biểu thức frac{1}{f}frac{1}{d}+frac{1}{d}
Đọc tiếp
Đố: Đặt vật sáng AB có độ cao h, vuông góc với trục chính của TKHT có tiêu cự f, điểm A nằm trên trục chính, cách thấu kính một khoảng d. Ảnh A'B' của vật AB có độ cao h' và hứng được trên màn cách thấu kính khoảng d'.
a) Chứng minh rằng độ phóng đại ảnh \(k=\frac{A'B'}{AB}=\frac{h'}{h}=\frac{d'}{d}\)
b) Chứng minh mối liên hệ giữa tiêu cự của thấu kính, khoảng các từ vật đến thấu kính và khoảng cách từ ảnh đến thấu kính tuân theo biểu thức \(\frac{1}{f}=\frac{1}{d}+\frac{1}{d'}\)
MÌNH THAM KHẢO NHÉ
a) Xét △ABO và △A′B′O có:
ABOˆ=A′B′Oˆ=900
BOAˆ=B′OA′ˆ (hai góc đối đỉnh)
⇒ Hai tam giác ABO và A'B'O là hai tam giác đồng dạng
⇒ \(\frac{A'B'}{AB}=\frac{B'O}{BO}\)
⇒ Độ phóng đại ảnh \(k=\frac{A'B'}{AB}=\frac{h'}{h}=\frac{d'}{d}\)
b) Tương tự: Hai tam giác A'B'F' và IOF' là hai tam giác đồng dạng
⇒\(\text{ }\frac{B'F'}{OF'}=\frac{A'B'}{IO}=\frac{d'}{d}\)
Áp dụng tính chất của tỉ lệ thức: \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)
⇒\(\frac{1}{f}=\frac{1}{d}=\frac{1}{f'}\)
CÓ MẤY CÁI KÍ HIỆU GÓC, MÌNH KHÔNG BIẾT VIẾT, BẠN THÔNG CẢM
a) Xét \(\Delta ABO\) và \(\Delta A'B'O'\)
\(ABO=A'B'O=90^0\)
\(BOA=B'O'A\)( hai góc đối đỉnh )
\(\Rightarrow\)Hai tam giác ABO và A'B'O là hai tam giác đồng dạng
\(\Rightarrow\frac{A'B}{AB}=\frac{B'O}{BO}\)
\(\Rightarrow\)Độ phóng đại ảnh : \(k=\frac{A'B}{AB}=\frac{h'}{h}=\frac{d'}{d}\)
b) Tương tự : Hai tam giác A'B'F và IOF' là hai tam giác đồng dạng
\(\Rightarrow\frac{B'F'}{OF}=\frac{A'B}{TO}=\frac{d'}{d}\)
Dựa vào tính chất của tỉ lệ thức : \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)
trang 79 SGK Toán 11 tập 1 - Chân trời sáng tạo
17 tháng 7 2023 lúc 13:16
Một thấu kính hội tụ có tiêu cự là f 0 không đổi. Gọi d và d lần lượt là khoảng cách từ vật thật và ảnh của nó tới quang tâm O của thấu kính (Hình 5). Ta có công thức: frac{1}{d} + frac{1}{{d}} frac{1}{f} hay d frac{{df}}{{d - f}}.Xét hàm số gleft( d right) frac{{df}}{{d - f}}. Tìm các giới hạn sau đây và giải thích ý nghĩa.a) mathop {lim }limits_{d to {f^ + }} gleft( d right); b) mathop {lim }limits_{d to + infty } gleft( d right).
Đọc tiếp
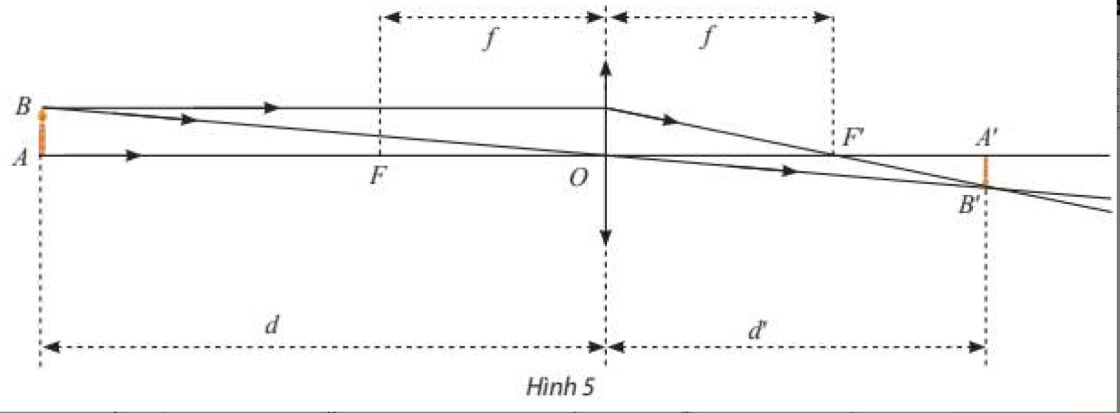
Một thấu kính hội tụ có tiêu cự là \(f > 0\) không đổi. Gọi \(d\) và \(d'\) lần lượt là khoảng cách từ vật thật và ảnh của nó tới quang tâm \(O\) của thấu kính (Hình 5). Ta có công thức: \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\) hay \(d' = \frac{{df}}{{d - f}}\).
Xét hàm số \(g\left( d \right) = \frac{{df}}{{d - f}}\). Tìm các giới hạn sau đây và giải thích ý nghĩa.
a) \(\mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right)\);
b) \(\mathop {\lim }\limits_{d \to + \infty } g\left( d \right)\).
a) \(\mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} = \mathop {\lim }\limits_{d \to {f^ + }} \left( {df} \right).\mathop {\lim }\limits_{d \to {f^ + }} \frac{1}{{d - f}}\)
Ta có: \(\mathop {\lim }\limits_{d \to {f^ + }} \left( {df} \right) = f\mathop {\lim }\limits_{d \to {f^ + }} d = {f^2};\mathop {\lim }\limits_{d \to {f^ + }} \frac{1}{{d - f}} = + \infty \)
\( \Rightarrow \mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} = + \infty \)
Ý nghĩa: Khi vật dần đến tiêu điểm từ phía xa thấu kính đến gần thấu kính thì khoảng cách từ ảnh đến thấu kính dần đến \( + \infty \).
b) \(\mathop {\lim }\limits_{d \to + \infty } g\left( d \right) = \mathop {\lim }\limits_{d \to + \infty } \frac{{df}}{{d - f}} = \mathop {\lim }\limits_{d \to + \infty } \frac{{df}}{{d\left( {1 - \frac{f}{d}} \right)}} = \mathop {\lim }\limits_{d \to + \infty } \frac{f}{{1 - \frac{f}{d}}} = \frac{f}{{1 - 0}} = f\)
Ý nghĩa: Khi khoảng cách từ vật đến thấu kính càng xa thì ảnh tiến dần đến tiêu điểm của ảnh \(\left( {F'} \right)\).
Đúng 0
Bình luận (0)
Một màn ảnh đặt song song với vật sáng AB và cách AB một đoạn L. Giữa vật và màn đặt một thấu kính hội tụ tiêu cự f có thể di chuyển được. Tiến hành di chuyển thấu kính thì thấy chỉ có 1 vị trí cho ảnh rõ nét trên màn. Mối liên hệ giữa L và f là A. L 1f B. L 4f C. L 2f D. L 3f
Đọc tiếp
Một màn ảnh đặt song song với vật sáng AB và cách AB một đoạn L. Giữa vật và màn đặt một thấu kính hội tụ tiêu cự f có thể di chuyển được. Tiến hành di chuyển thấu kính thì thấy chỉ có 1 vị trí cho ảnh rõ nét trên màn. Mối liên hệ giữa L và f là
A. L = 1f
B. L = 4f
C. L = 2f
D. L = 3f
Vật sáng AB có độ cao h= 2 cm, được đặt vuông góc trước một thấu kính hội tụ có tiêu cự d. Điểm A cách thấu kính một khoảng d=2f. Cho biết tiêu cự của thấu kính f=2cm A. Dựng ảnh A'B'của AB tạo bởi thấu kính hội tụ B. Tính chiều cao h'của ảnh và khoảng cách d'từ ảnh tới quang tâm.
Một màn ảnh đặt song song với vật sáng AB và cách AB một đoạn L. Một thấu kính hội tụ có tiêu cự f đặt trong khoảng giữa vật và màn sao cho AB vuông góc với trục chính của thấu kính. Tìm mối liên hệ giữa L và f để:a) có 2 vị trí của thấu kính cho ảnh rõ nét trên màn.b) có 1 vị trí của thấu kính cho ảnh rõ nét trên màn. c) không có vị trí của thấu kính cho ảnh rõ nét trên màn
Đọc tiếp
Một màn ảnh đặt song song với vật sáng AB và cách AB một đoạn L. Một thấu kính hội tụ có tiêu cự f đặt trong khoảng giữa vật và màn sao cho AB vuông góc với trục chính của thấu kính. Tìm mối liên hệ giữa L và f để:
a) có 2 vị trí của thấu kính cho ảnh rõ nét trên màn.
b) có 1 vị trí của thấu kính cho ảnh rõ nét trên màn.
c) không có vị trí của thấu kính cho ảnh rõ nét trên màn
Một màn ảnh đặt song song với vật sáng AB và cách AB một đoạn L. Một thấu kính hội tụ có tiêu cự f đặt trong khoảng giữa vật và màn sao cho AB vuông góc với trục chính của thấu kính. Tìm mối liên hệ giữa L và f để:a) có 2 vị trí của thấu kính cho ảnh rõ nét trên màn.b) có 1 vị trí của thấu kính cho ảnh rõ nét trên màn.c) không có vị trí của thấu kính cho ảnh rõ nét trên màn.
Đọc tiếp
Một màn ảnh đặt song song với vật sáng AB và cách AB một đoạn L. Một thấu kính hội tụ có tiêu cự f đặt trong khoảng giữa vật và màn sao cho AB vuông góc với trục chính của thấu kính. Tìm mối liên hệ giữa L và f để:
a) có 2 vị trí của thấu kính cho ảnh rõ nét trên màn.
b) có 1 vị trí của thấu kính cho ảnh rõ nét trên màn.
c) không có vị trí của thấu kính cho ảnh rõ nét trên màn.
b) Để có 1 vị trí của thấu kính cho ảnh rõ nét trên màn thì phương trình (*) phải có nghiệm kép nên:
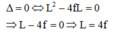
c) Để không có vị trí của thấu kính cho ảnh rõ nét trên màn thì phương trình (*) phải vô nghiệm nên:
Đúng 0
Bình luận (0)