Điều kiện là x 2   -   x   -   2   ≥   0

Điều kiện là x tùy ý.

Điều kiện là x tùy ý.

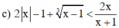
BPT xác định khi x + 1 ≠ 0 ⇔ x ≠ –1.

Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{–1}

a) Đkxđ: \(x-5\ne0\Leftrightarrow x\ne5\).
b) Đkxđ: \(x\in R\).
c) Đkxđ: \(x^2-x-2\ge0\)\(\Leftrightarrow\left(x+1\right)\left(x-2\right)\ge0\)
Th1: \(\left\{{}\begin{matrix}x-1\ge0\\x-2\ge0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x\ge2\end{matrix}\right.\)\(\Leftrightarrow x\ge2\).
Th2: \(\left\{{}\begin{matrix}x-1< 0\\x-2< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x< 1\\x< 2\end{matrix}\right.\)\(\Leftrightarrow x< 1\).
Đkxđ: \(\left[{}\begin{matrix}x\ge2\\x< 1\end{matrix}\right.\).
d) Đkxđ: \(x\in R\).

Đkxđ: \(\left\{{}\begin{matrix}5-x\ge0\\x-10>0\\\left(x-4\right)\left(x+5\right)\ne0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\le5\\x>10\\x\ne4\\x\ne-5\end{matrix}\right.\)\(\Leftrightarrow x\in\varnothing\).
Vậy BPT vô nghiệm.

Bất phương trình (1) :
Đkxđ: \(\left(x-1\right)\left(x-2\right)\ge0\)\(\Leftrightarrow\left[{}\begin{matrix}x\ge2\\x\le1\end{matrix}\right.\)
Bất phương trình (2):
Đkxđ: \(\left\{{}\begin{matrix}x-1\ge0\\x-2\ge0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x\ge2\end{matrix}\right.\)\(\Leftrightarrow x\ge2\).
Vậy hai bất phương trình không tương đương.

(2m + 1)x + m - 5 ≥ 0 ⇔ (2m + 1)x ≥ 5 - m (*)

TH1: 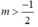 , bất phương trình (*) trở thành: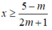 

Tập nghiệm của bất phương trình là:

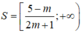
Để bất phương trình đã cho nghiệm đúng với ∀x ∈ (0;1)

thì (0;1)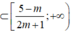 

Hay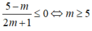 

TH2: 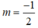 , bất phương trình (*) trở thành: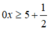 

Bất phương trình vô nghiệm. ⇒ không có m .

TH3: Với 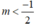 , bất phương trình (*) trở thành: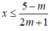 

Tập nghiệm của bất phương trình là:

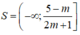
Để bất phương trình đã cho nghiệm đúng với ∀x ∈ (0;1)

thì (0;1)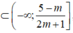 

Hay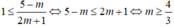 

Kết hợp điều kiện 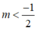 , ⇒ không có m thỏa mãn.

Vậy với m ≥ 5, bất phương trình đã cho nghiệm đúng với ∀x ∈ (0;1).