Chủ đề / Chương

Bài học

Hãy tham gia nhóm Học sinh Hoc24OLM
Bạn chưa đăng nhập. Vui lòng đăng nhập để hỏi bài
Pham Trong Bach
Tìm GTLN (max) của hàm số   y log 3 4 + 2 x - x 2 A.  log 3 4 B.  log 3 5 C.  5 3 D. ...
Đọc tiếp
Lớp 12 Toán
Những câu hỏi liên quan
Pham Trong Bach
Tìm GTLN (max) của hàm số  y x + 4 - x
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
19 tháng 6 2018 lúc 10:21

Chọn B

Bình luận (0)
Pham Trong Bach
Tìm GTLN (max); GTNN (min) của hàm số  y 2 x + 1 + 4 - x .
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
25 tháng 10 2019 lúc 15:06

Chọn B

Bình luận (0)
Pham Trong Bach
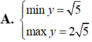
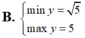
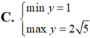
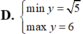
Tìm GTLN (max), GTNN (min) của hàm số y x + 2 x  với x ∈ 1 ; 3
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
30 tháng 11 2018 lúc 11:37

Chọn D

Bình luận (0)
Buddy

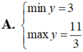
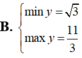
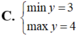
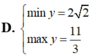
Tìm tập xác định của các hàm số sau:

a) \(y = \log \left| {x + 3} \right|;\)           

b) \(y = \ln \left( {4 - {x^2}} \right).\)

Xem chi tiết
Lớp 11 Toán Bài 20. Hàm số mũ và hàm số lôgarit

Khách
 
Hà Quang Minh
Hà Quang Minh Giáo viên CTVVIP
24 tháng 8 2023 lúc 0:57

a, \(y=log\left|x+3\right|\) có nghĩa khi \(\left|x+3\right|>0\)

Mà \(\left|x+3\right|\ge0\forall x\in R\)

\(\Rightarrow\) \(\left|x+3\right|>0\) khi \(x\ne-3\)

Vậy tập xác định của hàm số là D = R \ {-3}.

b, \(y=ln\left(4-x^2\right)\) có nghĩa khi \(4-x^2>0\)

\(\Rightarrow x^2< 4\\ \Leftrightarrow-2< x< 2\)

Vậy tập xác định của hàm số là D = (-2;2).

Bình luận (0)
Pham Trong Bach
Tìm GTLN (max), GTNN (min) của hàm số  y x + 2 x 2 + 1 trên  - 1 ; 1
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
1 tháng 12 2017 lúc 4:08

Chọn C

Bình luận (0)
Buddy

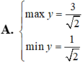
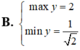
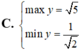
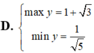
Tìm tập xác định của các hàm số:

a)     \(y = 12{}^x\)

b)    \(y = {\log _5}(2x - 3)\)

c)     \(y = {\log _{\frac{1}{5}}}\left( { - {x^2} + 4} \right)\)

Xem chi tiết
Lớp 11 Toán Bài 3. Hàm số mũ. Hàm số lôgarit

Khách
 
Hà Quang Minh
Hà Quang Minh Giáo viên CTVVIP
22 tháng 8 2023 lúc 11:31

\(a,D=R\\ b,2x-3>0\\ \Rightarrow x>\dfrac{3}{2}\\ \Rightarrow D=(\dfrac{3}{2};+\infty)\\ c,-x^2+4>0\\ \Rightarrow x^2< 4\\ \Leftrightarrow-2< x< 2\\ \Rightarrow D=\left(-2;2\right)\)

Bình luận (0)
Pham Trong Bach
Tìm GTLN (max), GTNN (min) của hàm số y x 3 - 2 x 2 - 4 x + 8 khi  x ∈ - 1 ; 1
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
24 tháng 10 2019 lúc 6:10

Chọn C

Bình luận (0)
Buddy

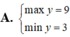
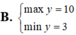
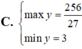
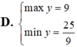
Cho đồ thị của hàm số \(y = {\log _2}x\) và y = 2 như Hình 6.8. Tìm khoảng giá trị của x mà đồ thị hàm số \(y = {\log _2}x\) nằm phía trên đường thẳng y = 2 và từ đó suy ra tập nghiệm của bất phương trình \({\log _2}x > 2.\)

Xem chi tiết
Lớp 11 Toán Bài 21. Phương trình, bất phương trình mũ và lôgar...

Khách
 
Hà Quang Minh
Hà Quang Minh Giáo viên CTVVIP
24 tháng 8 2023 lúc 1:01

Khoảng giá trị của x mà đồ thị hàm số \(y=log_2x\) nằm phía trên đường thẳng y = 2 là \(\left(4;+\infty\right)\)

\(\Rightarrow\) Tập nghiệm của bất phương trình \(log_2x>2\) là \(\left(4;+\infty\right)\)

Bình luận (0)
Pham Trong Bach
Tìm GTLN (max), GTNN (min) của hàm số y x 2 - 3 x - 2  trên  5 2 ; 5
Đọc tiếp
Xem chi tiết
Lớp 12 Toán

Khách
 
Cao Minh Tâm
Cao Minh Tâm
22 tháng 2 2018 lúc 7:54

Chọn B

Bình luận (0)
Buddy

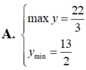
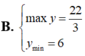
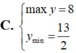
Tìm đạo hàm cấp hai của mỗi hàm số sau:

a)     \(y = \frac{1}{{2x + 3}}\)

b)    \(y = {\log _3}x\)

c)     \(y = {2^x}\)

Xem chi tiết
Lớp 11 Toán Bài 3. Đạo hàm cấp hai

Khách
 
Hà Quang Minh
Hà Quang Minh Giáo viên CTVVIP
22 tháng 8 2023 lúc 16:21

\(a,y'=\left(\dfrac{1}{2x+3}\right)'=-\dfrac{2}{\left(2x+3\right)^2}\\ \Rightarrow y''=\dfrac{2\cdot\left[\left(2x+3\right)^2\right]'}{\left(2x+3\right)^4}=\dfrac{8}{\left(2x+3\right)^3}\\ b,y'=\left(log_3x\right)'=\dfrac{1}{xln3}\\ \Rightarrow y''=-\dfrac{1}{x^2ln3}\\ c,y'=\left(2^x\right)'=2^x\cdot ln2\\ \Rightarrow y''=2^x\cdot\left(ln2\right)^2\)

Bình luận (0)