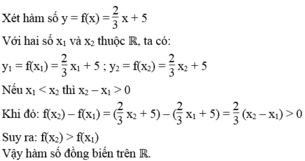Chứng minh rằng hàm số y = x x 2 + 1 đồng biến trên khoảng (-1; 1), nghịch biến trên khoảng (-∞; -1) và (1; +∞).

Những câu hỏi liên quan
Cho hàm số y = ( a 2 - 2a + 4)x - 9
Chứng minh rằng hàm số trên đồng biến trên R
y = ( a 2 - 2a + 4)x - 9
Ta có: a 2 - 2a + 4 = a 2 - 2a + 1 + 3 = a - 1 2 + 3 > 0 ∀a
Vậy hàm số luôn đồng biến trên R
Đúng 0
Bình luận (0)
Cho hàm số y = f(x) = 2 3 x + 5 với x ∈ R. Chứng minh rằng hàm số đồng biến trên R.
Cho f(x) = mx + 2014 và g(x) = ( m^2 + 1 )x + 2015. Chứng minh rằng hàm số y = f(x) + g(x) là số đồng biến trên R
Chứng minh rằng hàm số \(y=\dfrac{x^2}{x^2+1}\) đồng biến trên khoảng (-1 ; 1) và nghịch biến trên các khoảng (-∞ ; -1) và (1 ; +∞).
Tập xác định : D = R. y' = 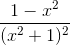 => y' = 0 ⇔ x=-1 hoặc x=1.
=> y' = 0 ⇔ x=-1 hoặc x=1.
Bảng biến thiên :
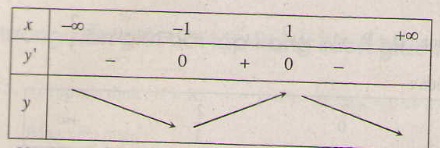
Vậy hàm số đồng biến trên khoảng (-1 ; 1); nghịch biến trên các khoảng (-∞ ; -1), (1 ; +∞).
Đúng 0
Bình luận (0)
Chứng minh rằng hàm số \(y=\sqrt{2x-x^2}\) đồng biến trên khoảng (0 ; 1) và nghịch biến trên các khoảng (1 ; 2).
Tập xác định : D = [0 ; 2]; y' = , ∀x ∈ (0 ; 2); y' = 0 ⇔ x = 1.
Bảng biến thiên :
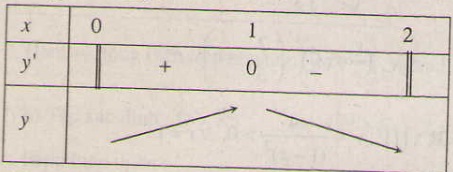
Vậy hàm số đồng biến trên khoảng (0 ; 1) và nghịch biến trên khoảng (1 ; 2).
Đúng 0
Bình luận (0)
Chứng minh rằng : hàm số y=f(x)=1/2x+1 đồng biến trên R
Với \(x_1;x_2\)bất kì thuộc \(ℝ\)và \(x_1< x_2\) Ta có :
\(f\left(x_1\right)=\frac{1}{2}x_1+1\)
\(f\left(x_2\right)=\frac{1}{2}x_2+1\)
\(\Rightarrow f\left(x_1\right)-f\left(x_2\right)=\frac{1}{2}\left(x_1-x_2\right)< 0\)
(Vì \(x_1< x_2\Rightarrow x_1-x_2< 0\))
\(\Rightarrow f\left(x_1\right)< f\left(x_2\right)\)
Vậy hàm số đồng biến trên \(ℝ\)
Đúng 0
Bình luận (0)
Cho hàm số \(y=2x^2-8x+1\). Chứng minh rằng hàm số nghịch biến khi x < 2, đồng biến khi x > 2
Chứng minh rằng hàm số y = 2 x - x 2 đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).
TXĐ: D = [0; 2]
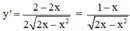
+ Hàm số đồng biến
⇔ y’ > 0
⇔ 0 < x < 1.
+ Hàm số nghịch biến
⇔ y’ < 0
⇔ 1 < x < 2.
Vậy hàm số đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).
Đúng 0
Bình luận (0)
Cho hàm số \(y=\left(3m^2-7m+5\right)x-2011\). Chứng minh rằng hàm số trên luôn đồng biến trên R với mọi m
Chứng minh rằng hàm số \(y=x^3+x\) đồng biến trên R
Áp dụng giải phương trình sau \(x^3-x=\sqrt[3]{2x+1}+1\)
Hi guys, please help me
i need it now !!!
Lời giải
$y'=3x^2+1>0$ với mọi $x\in\mathbb{R}$ nên hàm $y=x^3+x$ đồng biến trên $\mathbb{R}$
PT $\Leftrightarrow x^3+x=\sqrt[3]{2x+1}+2x+1$
Đặt $\sqrt[3]{2x+1}=t$ thì:
$x^3+x=t^3+t$
Vì hàm $y=x^3+x$ đồng biến nên $x^3+x=t^3+t\Leftrightarrow x=t$
$\Leftrightarrow x=\sqrt[3]{2x+1}$
$\Leftrightarrow x^3=2x+1$
Giải pt này dễ dàng có $x=-1; \frac{1\pm \sqrt{5}}{2}$
Đúng 1
Bình luận (0)