Cho hàm số f x = tan x − 2 π 3 . Giá trị f ' 0 bằng
A. − 3
B. 4
C. -3
D. 3
Tìm hàm số F(x) sao cho F’(x) = f(x) nếu:
f(x) = 1/(cosx)2 với x ∈ ((-π)/2; π/2). f x = 1 cos x 2 v ớ i x ∈ - π 2 ; π 2
Cho hàm số f ( x ) = 1 + c o s x ( x - π ) 2 k h i x ≠ π m k h i x = π Tìm m để f(x) liên tục tại x = π
A. m = 1 4
B. m = - 1 4
C. m = 1 2
D. m = - 1 2
Cho hàm số f(x) = sin3x.
Tính f''(-π/2), f''(0), f''(π/18)
f''(-π/2) = -9, f''(0) = 0, f''(π/18) = -9/2
Cho các mệnh đề sau
(I) Hàm số f(x) = sin x x 2 + 1 là hàm số chẵn.
(II) Hàm số f(x) = 3sinx + 4cosx có giá trị lớn nhất là 5.
(III) Hàm số f(x) = tanx tuần hoàn với chu kì 2 π .
(IV) Hàm số f(x) = cosx đồng biến trên khoảng (0; π )
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?
A. 4
B. 2
C. 3
D. 1
Cho hàm số f(x) thỏa mãn ∫ 0 π f ' ( x ) d x = 1 , f ( 0 ) = π . Tính f ( π )
A. f ( π ) = 1 - π
B. f ( π ) = π - 1
C. f π = π + 1
D. f π = - π - 1
Có f ( π ) - f ( 0 ) = ∫ 0 π f ' ( x ) dx
f ( π ) = f ( 0 ) + ∫ 0 π f ' ( x ) dx = π + 1
Chọn đáp án C.
Cho F ( x ) = cos 2 x - sin x + C là nguyên hàm của hàm số f(x). Tính f ( π )
A. f ( π ) = - 3
B. f ( π ) = 1
C. f ( π ) = - 1
D. f ( π ) = 0
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = 2 cos x - 1 sin 2 x trên khoảng 0 ; π . Biết rằng giá trị lớn nhất của F(x) trên khoảng 0 ; π là 3 . Chọn mệnh đề đúng trong các mệnh đề sau?

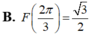
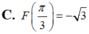
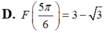
Cho hàm f(x) có đạo hàm trên đoạn [ 0 ; π ] , f ( 0 ) = π , ∫ 0 π f ' ( x ) dx = 3 π . Tính f ( π )
![]()
![]()
![]()
![]()
Cho hàm f(x) có đạo hàm trên đoạn [ 0 ; π ] , f ( 0 ) = π , ∫ 0 π f ' ( x ) dx = 3 π . Tính f ( π )
A. f ( π ) = 0
B. f ( π ) = - π
C. f ( π ) = 4 π
D. f ( π ) = 2 π
Tính đạo hàm của hàm số: y = tan π / 2 – x với x ≠ k π , k ∈ Z
Đặt u = π/2 - x thì u' = -1
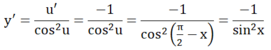
Do cos(π/2-x) = sinx