Cho hàm số y = 4 x − x . Nghiệm của phương trình y’ = 0 là
A. x = 1 8
B. x = 1 2
C. x = 1 64
D. x = 1 4
cho hàm số y = \(3x^4\)- \(3x^2\) - 6\(x\) + 1 nghiệm của phương trình y' = 0 là
\(y'=12x^3-6x-6\)
\(=6\left(2x^3-x-1\right)=6\left(x-1\right)\left(2x^2+2x+1\right)\)
\(\Rightarrow\) Nghiệm của pt \(y'=0\) là \(x=1\)
Cho hàm số y = f ( x ) = ln ( 1 + x 2 + x ) .
Tập nghiệm của bất phương trình
f ( a - 1 ) + f ( ln a ) ≤ 0 là:
![]()
![]()
![]()
![]()
Cho hàm số y = x 2 + x + 2 x - 1 Tập nghiệm của bất phương trình y’ < 0 là
A. [-1;3]
B. [-1;3] \ {1}
C. (-1;3)\{1}
D. (-1;3)
Cho hàm số y = x 2 + x + 2 x - 1 . Tập nghiệm của bất phương trình y’ < 0 là
A. [-1;3]
B. [-1;3] \ {1}
C. (-1;3)\{1}
D. (-1;3)
Cho hàm số y = f(x) có bảng biến thiên như sau.
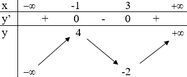
Số nghiệm của phương trình f 2 ( x ) - 4 = 0 là
A. 3.
B. 5.
C. 1.
D. 2.
Cho hàm số y = f(x) có bảng biến thiên như sau
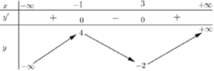
Số nghiệm của phương trình f(x) – 4 = 0 là
A. 2.
B. 3.
C. 0.
D. 1.
Cho hàm số y =f(x) có bảng biến thiên như sau
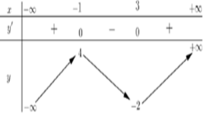
Số nghiệm của phương trình f(x) - 4 =0 là
A. 2
B. 3
C. 0
D. 1
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
Cho hàm số f ( x ) = a x 4 + b x 2 - 1 ( a , b ∈ ℝ ) . Đồ thị của hàm số y=f(x) như hình vẽ bên. Số nghiệm thực của phương trình 2018.f(x) + 2019 = 0 là:
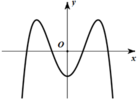
A. 4
B. 0
C. 3
D. 2