Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB=BC=a 3 , S A B ^ = S C D ^ = 90 0 và khoảng cách từ điểm A đến mặt phẳng (SBC) bằng a 2 . Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC theo a.
![]()
![]()
![]()
![]()
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = a cạnh bên SA vuông góc với đáy và SA = a. Tính diện tích toàn phần S t p của hình chóp S.ABC.
A. S t p = 2 a 2
B. S t p = a 2 1 + 2
C. S t p = a 2 1 + 2 2
D. S t p = 2 a 2 2
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, A B = B C = a , cạnh bên SA vuông góc với đáy và SA = a. Tính diện tích toàn phần S t p của hình chóp S.ABC.
![]()
![]()
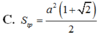
![]()
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B có AB=BC=a,SB=2a và SA vuông góc với đáy. Tính thể tích khối chóp S.ABC.
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450.
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Đáp án C
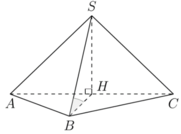
Gọi H là trung điểm AC. Ta có tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC)
suy ra S H ⊥ A B C
Ta có
S B , A B C = S B H ^ = 45 o ⇒ S H = B H = 1 2 A C = a 2 2 V S . A B C = 1 3 . a 2 2 . 1 2 a 2 = a 3 2 12
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, BC=2a. Mặt bên SBC là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Thể tích khối chóp S.ABC là
A . V = a 3
B . V = 2 a 3 3
C . V = 2 a 3 3
D . a 3 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = 2a. Tam giác SAC cân tại S có đường cao và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách giữa hai đường thẳng AB và SC theo a.
A . a 3 3
B . 2 a 3
C . a 3 2
D . a
Đáp án A.
Theo giả thiết ta có SO ⊥ (ABC). Gọi D là điểm đối xưng với B qua O
=> ABCD là hình vuông => AB//CD
=> d(AB;SC) = d(AB;(SCD)) = d(E;(SCD)) = 2d(O;(SCD))(Với E, F lần lượt là trung điểm của AB và CD).
Áp dung tính chất tứ diện vuông cho tứ diện OSCD ta có:
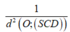
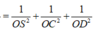
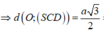
![]()
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = 2a. Tam giác SAC cân tại S có đường cao S O = a 3 và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách giữa hai đường thẳng AB và SC theo a
A. a 3 3 .
B. 2 a 3 .
C. a 3 2 .
D. a
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, AB = AC= a; mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC
A. 1 12 a 3
B. 3 4 a 3
C. 3 12 a 3
D. 1 4 a 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân, A B = A C = a ; mặt bên SAB là tam giác vuông cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích của khối chóp S.ABC.
A. 1 12 a 3
B. 3 4 a 3
C. 3 12 a 3
D. 1 4 a 3
Đáp án A
Gọi H là trung điểm của AB suy ra S H ⊥ A B
Do Δ S A B vuông cân tại S nên S H = A B 2 = a 2 ; S A B C = a 2 2 ⇒ V = a 3 12 .