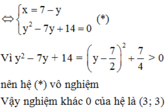Hãy chỉ ra một nghiệm của bất phương trình 2x + 4 < 0

Những câu hỏi liên quan
Chỉ ra một nghiệm của hệ bất phương trình sau: \(\left\{ \begin{array}{l}2x + y > 0\\x - 3y < 6\\x - y \ge - 4\end{array} \right.\)
Thay x=1; y=1 vào 3 bất phương trình ta được:
\(2.1 + 1 > 0\) (Đúng)
\(1 - 3.1 < 6\) (Đúng)
\(1 - 1 \ge - 4\) (Đúng)
Vậy (1;1) là một nghiệm của hệ bất phương trình đã cho.
Đúng 0
Bình luận (0)
Cho bất phương trình bậc nhất hai ẩn \(x + 2y \ge 0\).
a) Hãy chỉ ra ít nhất hai nghiệm của bất phương trình trên.
b) Với y=0, có bao nhiêu giá trị của x thỏa mãn bất phương trình đã cho?
a)
+) Thay x=0 và y=0 vào bất phương trình \(x + 2y \ge 0\), ta được:
\(0 + 2.0 \ge 0 \Leftrightarrow 0 \ge 0\)(Đúng)
=> (0;0) là một nghiệm của bất phương trình \(x + 2y \ge 0\)
+) Thay x=1, y=1 vào bất phương trình \(x + 2y \ge 0\) ta được:
\(1 + 2.1 \ge 0 \Leftrightarrow 3 \ge 0\)(Đúng)
=> (1;1) là một nghiệm của bất phương trình \(x + 2y \ge 0\)
Ta tìm được 2 nghiệm của bất phương trình đã cho là (0;0) và (1;1).
b)
Thay y=0 vào bất phương trình \(x + 2y \ge 0\) ta được:
\(x + 2.0 \ge 0 \Leftrightarrow x \ge 0\)
Ta thấy bất phương trình bài cho tương đương với bất phương trình nên số giá trị của x thỏa mãn bất phương trình đã cho là số x thỏa mãn điều kiện .
Mà ta có vô số giá trị của x thỏa mãn nên có vô số giá trị của x thỏa mãn bất phương trình đã cho.
Chú ý
Ta có thể thử các cặp số khác đối với câu a, miễn là cặp số đấy làm cho bất phương trình đúng.
Đúng 0
Bình luận (0)
Cho bất phương trình bậc nhất hai ẩn \(x - 2y + 6 > 0\)
a) (0;0) có phải là một nghiệm của bất phương trình đã cho không?
b) Chỉ ra ba cặp số (x;y) là nghiệm của bất phương trình đã cho.
c) Biểu diễn miền nghiệm của các bất phương trình đã cho trên mặt phẳng tọa độ Oxy
Tham khảo:
a) Vì \(0 - 2.0 + 6 = 6 > 0\) nên (0;0) là một nghiệm của bất phương trình đã cho.
b) Vì \(0 - 2.1 + 6 = 4 > 0\) nên (0;1) là một nghiệm của bất phương trình đã cho.
Vì \(1 - 2.0 + 6 = 7 > 0\) nên (1;0) là một nghiệm của bất phương trình đã cho.
Vì \(1 - 2.1 + 6 = 5 > 0\) nên (1;1) là một nghiệm của bất phương trình đã cho.
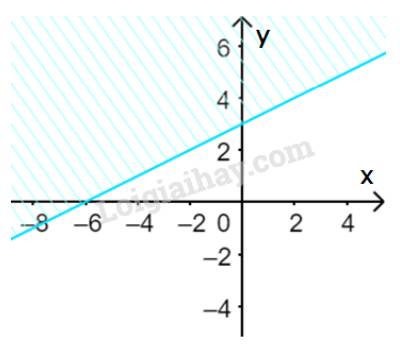
c) Vẽ đường thẳng \(\Delta :x - 2y + 6 = 0\) đi qua hai điểm \(A(0;3)\) và \(B\left( { - 2;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 - 2.0 + 6 = 6 > 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
Đúng 0
Bình luận (0)
Hãy chỉ ra một nghiệm của bất phương trình trong ví dụ của câu hỏi 2 ?
Ví dụ: 2x + 4 < 0
⇔ 2x < -4 ⇔ x < -2
Ví dụ -3 là một nghiệm của bất phương trình này.
Đúng 0
Bình luận (0)
Viết các tập hợp sau đây dưới dạng chỉ ra tính chất đặc trưng cho các phần tử:
a) Tập hợp \(A = \{1;2;3;6;9;18\} \)
b) Tập hợp \(B\) các nghiệm của bất phương trình \(2x+1>0\)
c) Tập hợp \(C\) các nghiệm của phương trình \(2x-y=6\)
a) A là tập hợp các ước nguyên dương của 18.
\(A = \{x \in \mathbb N | x \in U(18)\} \)
b) \(B = \{x \in \mathbb R | 2x+1>0\} \)
c) C là tập hợp các cặp số (x;y) thỏa mãn \(2x-y=6\).
\(C = \{(x;y)| 2x-y=6\} \)
Đúng 0
Bình luận (0)
Hãy chỉ ra cặp nghiệm khác 0 của hệ phương trình
x
2
5
x
-
2
y
y
2
5
y
-...
Đọc tiếp
Hãy chỉ ra cặp nghiệm khác 0 của hệ phương trình x 2 = 5 x - 2 y y 2 = 5 y - 2 x
A. (3; 3)
B. (2; 2); (3; 1); (-3; 6)
C. (1; 1); (2; 2); (3; 3)
D. (-2; -2); (1; -2); (-6; 3)
Đáp án A

Vậy nghiệm khác 0 của hệ là (3; 3).
Đúng 0
Bình luận (0)
Hãy chỉ ra các cặp nghiệm khác 0 của hệ phương trình
x
2
5
x
-
2
y
y
2
5
y...
Đọc tiếp
Hãy chỉ ra các cặp nghiệm khác 0 của hệ phương trình x 2 = 5 x - 2 y y 2 = 5 y - 2 x
A. (3; 3)
B. (2; 2); (3; 1); (−3; 6)
C. (1; 1); (2; 2); (3; 3)
D. (−2; −2); (1; −2); (−6; 3)
Hệ bất phương trình
2
x
-
4
0
m
x
-
1
0
có tập nghiệm là (2;
+
∞
) khi và chỉ khi A. m 0 B. ...
Đọc tiếp
Hệ bất phương trình 2 x - 4 > 0 m x - 1 < 0 có tập nghiệm là (2; + ∞ ) khi và chỉ khi
A. m < 0
B. m ≤ 0
C. m = 1 2
D. m > 0
Ta có 2x – 4 >0
* Xét bất phương trình: mx – 1 <0 (*)
+ Nếu m = 0 thì ( *) luôn đúng với mọi x.
Khi đó, tập nghiệm của hệ bất phương trình là ( 2 ; + ∞ ) .
+ Nếu m > 0 thì từ (*) ⇔ m x < 1 ⇔ x < 1 m
Trong trường hợp này thì tập nghiệm của hệ bất phương trình không thể là ( 2 ; + ∞ ) .
+ Nếu m < 0 thì từ (*) ⇔ m x < 1 ⇔ x < 1 m
Do đó, để hệ bất phương trình đã cho có tập nghiệm là ( 2 ; + ∞ ) khi và chỉ khi 1 m < 2 ( luôn đúng vì m < 0).
Vậy tập hợp các giá trị m thỏa mãn là m ≤ 0 .
Đúng 0
Bình luận (0)
Giải bất phương trình -2x + 3 > 0 và biểu diễn trên trục số tập nghiệm của nó
Từ đó hãy chỉ ra các khoảng mà nếu x lấy giá trị trong đó thì nhị thức f(x) = -2x + 3 có giá trị
Trái dấu với hệ số của x;
Cùng dấu với hệ số của x.
-2x + 3 > 0 ⇔ -2x > -3 ⇔ x < 3/2
Biểu diễn tập nghiệm trên trục số:
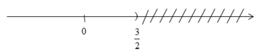
Nhị thức f(x) = -2x + 3 có giá trị:
Trái dấu với hệ số của x khi x < 3/2
Cùng dấu với hệ số của x khi x > 3/2
Đúng 0
Bình luận (0)