Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = - 70 o với A(1; 0). Gọi M 1 là điểm đối xứng của M qua đường phân giác của góc phần tư thứ I. Số đo của cung lượng giác A M 1 là
A . - 150 ο B . 220 ο C . 160 ο D . - 160 ο
Những câu hỏi liên quan
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM
80
o
trong đó A(1; 0). Gọi M là điểm đối xứng với M qua đường phân giác của góc phần tư thứ II. Số đo của cung lượng giác AM là: A.
170
o
B.
-
200
o
C.
190
o
D.
280
o
Đọc tiếp
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = 80 o trong đó A(1; 0). Gọi M' là điểm đối xứng với M qua đường phân giác của góc phần tư thứ II. Số đo của cung lượng giác AM' là:
A. 170 o B. - 200 o
C. 190 o D. 280 o
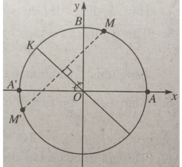
Sđ MK = sđ KM’ = 55 o
⇒ sđ AM’ = sđ AM + sđ MK + sđ KM’ = 190 o .
Đáp án: C
Đúng 0
Bình luận (0)
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM α, π/2 α π, A(1; 0). Gọi
M
2
là điểm đối xứng với M qua trục Ox. Số đo của cung
A
M
3
là A. π - α + k2π, k ∈ Z B. α + π/2 + k2π, k ∈ Z C. α - π + k2π, k ∈ Z D. -α + k2π, k ∈ Z
Đọc tiếp
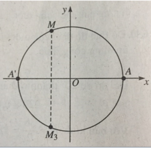
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π/2 < α < π, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 3 là
A. π - α + k2π, k ∈ Z B. α + π/2 + k2π, k ∈ Z
C. α - π + k2π, k ∈ Z D. -α + k2π, k ∈ Z
-π = -3,14; -2π = -6,28; (-5π)/2 = -7,85.
Vậy (-5π)/2 < -6,32 < -2π.
Do đó điểm M nằm ở góc phần tư thứ II.
Đáp án: B
Đúng 0
Bình luận (0)
Trên đường tròn lượng giác, với điểm gốc A, hãy xác định các điểm M mà số đo của cung AM bằng x (rad) tương ứng đã cho ở trên và xác định sinx, cosx (lấy π ≈ 3,14)
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM α, π α 3π/2, A(1; 0). Gọi
M
2
là điểm đối xứng với M qua trục Ox. Số đo của cung A
M
2
là A. α - π + k2π, k ∈ Z B. π - α + k2π, k ∈ Z C. 2π - α + k2π, k ∈ Z D. 3π/2 - α + k2π, k ∈ Z
Đọc tiếp
Trên đường tròn lượng giác cho điểm M xác định bởi số đo AM = α, π < α < 3π/2, A(1; 0). Gọi M 2 là điểm đối xứng với M qua trục Ox. Số đo của cung A M 2 là
A. α - π + k2π, k ∈ Z B. π - α + k2π, k ∈ Z
C. 2π - α + k2π, k ∈ Z D. 3π/2 - α + k2π, k ∈ Z
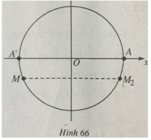
(h.66) Ta có
A M 2 = MA’ = MA + AA’
Suy ra
Sđ A M 2 = -α + π + k2π, k ∈ Z.
Vậy đáp án là B.
6.13. (h.67) Ta có
Sđ A M 3 = -sđ AM = -α + k2π, k ∈ Z.
Đáp án: D
Đúng 0
Bình luận (0)
Trên đường tròn lượng giác cho điểm M xác định bởi sđ cung AM = α (0 < α < π/2). Gọi M1, M2, M3 lần lượt là điểm đối xứng của M qua trục Ox, trục Oy và gốc tọa độ. Tìm số đo các cung AM1, AM2, AM3.
Cho đường tròn(O;R) đường kính AB và C là điểm nằm trên đường tròn. Gọi M là điểm đối xứng với A qua C
a)Hãy xác định vị trí điểm C trên (O;R) sao cho AM lớn nhất
b)Cho biết AM= 2R\(\sqrt{3}\). Hãy tìm số đo góc A
c)CMR M thuộc 1 đươngf tròn cố định khi C chạy trên (O;R)
Trên đường tròn lượng giác gốc A, xác định các điểm M khác nhau biết rằng cung AM có số đo tương ứng là (trong đó k là một số nguyên tùy ý)
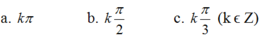
a) Nếu k = 2n +1 (n ∈ Z) (thì kπ = (2n + 1)π = 2nπ + π nên M ≡ M1
Nếu k = 2n (n ∈ Z) thì kπ = 2nπ nên M ≡ A
b)
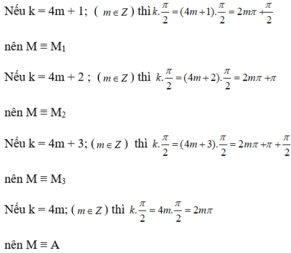
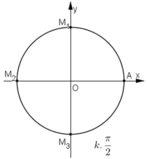
c)
Đúng 0
Bình luận (0)
Giải mục 1 trang 7 ,8 , 9 SGK Toán 11 tập 1 - Chân trời sáng tạo
16 tháng 7 2023 lúc 16:43
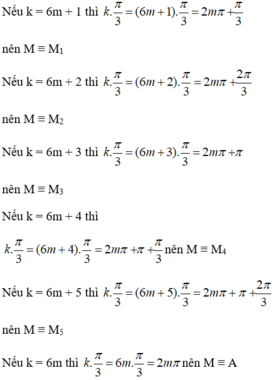
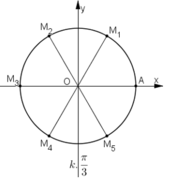
Trong mặt phẳng tọa độ Oxy, vẽ đường tròn tâm O bán kính bằng 1 và điểm A(1; 0).
a) Cho điểm B(0; 1). Số đo góc lượng giác (OA; OB) bằng bao nhiêu radian?
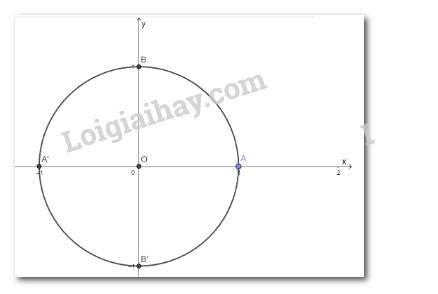
b) Xác định các điểm A’ và B’ trên đường tròn sao cho các góc lượng giác (OA; OA’), (OA, OB’) có số đo lần lượt là \(\pi \,\) và \( - \frac{\pi }{2}\)
Tham khảo:
a)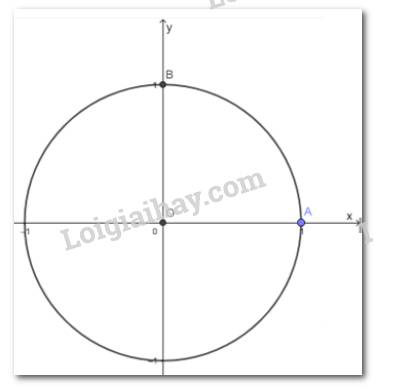 
Góc lượng giác \(\left( {OA;OB} \right) = 90^\circ = \frac{\pi }{2}\)
b)
Đúng 0
Bình luận (0)
Cho góc lượng giác có số đo bằng \(\frac{{5\pi }}{6}\)
a) Xác định điểm M trên đường tròn lượng giác biểu diễn góc lượng giác đã cho.
b) Tính các giá trị lượng giác của góc lượng giác đã cho.
Tham khảo:
a) Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó điểm M là điểm biểu diễn bởi góc có số đo \(\frac{{5\pi }}{6}\)
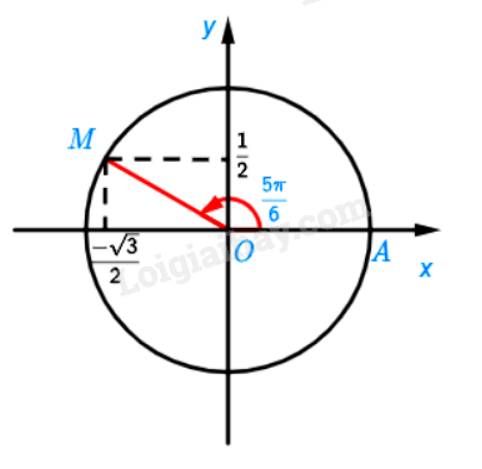
b) Ta có:
\(\sin \left( {\frac{{5\pi }}{6}} \right) = \frac{1}{2};\cos \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{2};\tan \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - \sqrt 3 }}{3};\cot \left( {\frac{{5\pi }}{6}} \right) = \frac{{ - 3}}{{\sqrt 3 }}\)
Đúng 0
Bình luận (0)