Phát biểu các định lí về quan hệ vuông góc giữa đường kính và dây.

Những câu hỏi liên quan
Phát biểu các định lí về quan hệ vuông góc giữa đường kính và dây ?
Nếu một đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy. Ngược lại, một đường kính đi qua trung điểm của một dây không phải là đường kính thì vuông góc với dây ấy.
Đúng 0
Bình luận (0)
Phát biểu các định lí về mối quan hệ giữa cung nhỏ và dây căng cung đó trong một đường tròn.
Với hai cung nhỏ của một đường tròn hay hai đường tròn bằng nhau thì:
- Hai cung bằng nhau căng hai dây bằng nhau.
- Hai dây bằng nhau căng hai cung bằng nhau.
- Cung lớn hơn căng dây lớn hơn.
- Dây lớn hơn căng cung lớn hơn.
Đúng 0
Bình luận (0)
Phát biểu các định lí về mối quan hệ giữa cung nhỏ và dây căng cung đó trong một đường tròn.
Với hai cung nhỏ của một đường tròn hay hai đường tròn bằng nhau thì:
- Hai cung bằng nhau căng hai dây bằng nhau.
- Hai dây bằng nhau căng hai cung bằng nhau.
- Cung lớn hơn căng dây lớn hơn.
- Dây lớn hơn căng cung lớn hơn.
Đúng 0
Bình luận (0)
Phát biểu các định lí về liên hệ giữa dây và khoảng cách từ tâm đến dây.
Trong một đường tròn:
- Hai dây bằng nhau thì cách đều tâm và ngược lại, hai dây cách đều tâm thì bằng nhau.
- Dây lớn hơn thì gần tâm hơn và ngược lại, dây gần tâm hơn thì lớn hơn.
Đúng 0
Bình luận (0)
Phát biểu các định lí về liên hệ giữa dây và khoảng cách từ tâm đến dây ?
Trong một đường tròn:
- Hai dây bằng nhau thì cách đều tâm và ngược lại, hai dây cách đều tâm thì bằng nhau.
- Dây lớn hơn thì gần tâm hơn và ngược lại, dây gần tâm hơn thì lớn hơn.
Đúng 0
Bình luận (0)
Định lý về mối quan hệ giữa đường kính và dây của đường tròn
định lí quan hệ giữa đường vuông góc và đường xiên
Định lý 1: Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Định lý 2: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó;
a) Đường xiên nào có hình chiếu lớn hơn thì lớn hơn
b) Đường xiên nào lớn hơn thì có hình chiếu lớn hơn
c) Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau và ngược lại nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.
Đúng 0
Bình luận (0)
Câu 1: Phát biểu định nghĩa hai góc đối đỉnh (Vẽ hình)Câu 2: Phát biểu định lí hai góc đối đỉnhCâu 3: phát biểu định nghĩa hai đường thẳng vuông gócCâu 4: Phát biểu định nghĩa đường trung trực của đoạn thẳngCâu 5: Phát biểu dấu hiệu (định lí) nhận bik hai đường thẳng song songCâu 6: Phát biểu tiên đề ơ clít về đường thẳng song songCâu 7: Phát biểu tính chất (định lí) của hai đường thẳng song songCâu 8: Phát biểu định lí về hai đường thẳng phân biệt với một đường thẳng số 3Câu 9: Phát biểu định l...
Đọc tiếp
Câu 1: Phát biểu định nghĩa hai góc đối đỉnh (Vẽ hình)
Câu 2: Phát biểu định lí hai góc đối đỉnh
Câu 3: phát biểu định nghĩa hai đường thẳng vuông góc
Câu 4: Phát biểu định nghĩa đường trung trực của đoạn thẳng
Câu 5: Phát biểu dấu hiệu (định lí) nhận bik hai đường thẳng song song
Câu 6: Phát biểu tiên đề ơ clít về đường thẳng song song
Câu 7: Phát biểu tính chất (định lí) của hai đường thẳng song song
Câu 8: Phát biểu định lí về hai đường thẳng phân biệt với một đường thẳng số 3
Câu 9: Phát biểu định lí về hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba
Câu 10: Phát biểu định lí về một đường thẳng vuông góc với một đường thẳng song song
Câu 11: Phát biểu định lí về tổng ba góc của một tam giác
Câu 12: phát biểu tính chất góc ngoài của tam giác, phát biểu ba trường hợp bằng nhau của tam giác
Câu 13: phát biểu các trường hợp bằng nhau của tam giác vuông
(Mọi người ơi mọi người giúp em mấy câu hỏi này với😅Thank you m.n)
vote cho mk xong rồi mk trả lời cho, tin mk đi, mk ko phải n xấu đâu
a) Chứng minh định lí : Đường kính đi qua điểm chính giữa của 1 cung thì đi qua trung điểm của dây căng cung ấy
b) Phát biểu định lí đảo
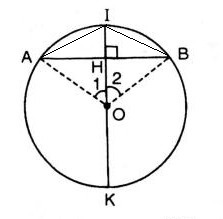
vì Ià điểm chính giữa của cung AB,suy ra:\(\widehat{IA}=\widehat{IB}\)
Ta có: OA=OB=bán kính. Suy ra đường kính IK là đường trung trực của dây ABAB. Vậy HA=HB (đpcm)
b,Mệnh đề đảo: Đường kính đi qua trung điểm của một dây thì đi qua điểm chính giữa của cung căng dây đó.












