Cho elip có phương trình 4 x 2 + 9 y 2 = 36 . Khi đó hình chữ nhật cơ sở có diện tích bằng:
A. 6
B. 12
C. 24
D. 36
Những câu hỏi liên quan
Cho elip có phương trình 4 x 2 + 9 y 2 = 36. Khi đó, hình chữ nhật cơ sở có diện tích bằng:
A. 6
B. 12
C. 24
D. 36
Đáp án: C
4 x 2 + 9 y 2 = 36
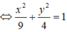
Elip có a 2 = 9 ⇒ a = 3, b 2 = 4 ⇒ b = 2
Hình chữ nhật cơ sở có hai cạnh là 2a = 6, 2b = 4. Do đó, diện tích hình chữ nhật cơ sở là: 6.4 = 24
Đúng 0
Bình luận (0)
Cho elip có phương trình 4 x 2 + 9 y 2 = 1 . Khi đó hình chữ nhật cơ sở có diện tích bằng:
A. 6
B. 1/6
C. 24
D. 2/3
Cho elip có phương trình: 16 x 2 + 25 y 2 = 400 . Khi đó chu vi hình chữ nhật cơ sở là:
A. 9
B. 18
C. 36
D. 48
Cho elip có phương trình 16 x 2 + m y 2 = 400 c có chu vi hình chữ nhật cơ sở là 30. Khi đó m nhận giá trị là:
A. 9
B. 25
C. 64
D. 100
Cho Elip có phương trình : 9x2+ 25y2 225. Lúc đó hình chữ nhật cơ sở có diện tích bằng A. 20 B. 35 C. 60 D. 40
Đọc tiếp
Cho Elip có phương trình : 9x2+ 25y2= 225. Lúc đó hình chữ nhật cơ sở có diện tích bằng
A. 20
B. 35
C. 60
D. 40
Ta có
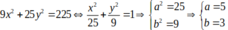
Độ dài trục lớn ( chiều dài hình chữ nhật cơ sở ): 2a= 10 .
Độ dài trục nhỏ ( chiều rộng hình chữ nhật cơ sở : 2b= 6
Diện tích hình chữ nhật cơ sở là 2a. 2b= 10.6= 60 .
Chọn C.
Đúng 0
Bình luận (0)
Phương trình
x
2
m
2
+
y
2
36
1
là phương trình chính tắc của elip có hình chữ nhật cơ sở với diện tích bằng 300 thì: A.
m
±
5
2
B.
m
±
15
2...
Đọc tiếp
Phương trình x 2 m 2 + y 2 36 = 1 là phương trình chính tắc của elip có hình chữ nhật cơ sở với diện tích bằng 300 thì:
A. m = ± 5 2
B. m = ± 15 2
C. m = ± 25 2
D. Không tồn tại m
Tìm phương trình chính tắc của Elip có một đỉnh của hình chữ nhật cơ sở là M(4;3) A. B. C. D.
Đọc tiếp
Tìm phương trình chính tắc của Elip có một đỉnh của hình chữ nhật cơ sở là M(4;3)
A. 
B. 
C. 
D. 
Gọi phương trình chính tắc của Elip có dạng
Các đỉnh của hình chữ nhật cơ sở có tọa độ: (a; b) ; (a; -b) ; ( -a; b) và (-a; -b)
Ta có M( 4;3) là một đỉnh của hình chữ nhật cơ sở nên chọn
.
=> phương trình chính tắc của (E) là
Chọn A.
Đúng 0
Bình luận (0)
Phương trình chính tắc của elip có độ dài trục nhỏ bằng 8, hình chữ nhật cơ sở có chu vi bằng 40 là: A.
x
2
36
+
y
2
16
1
B.
36
x
2
+
16
y
2
...
Đọc tiếp
Phương trình chính tắc của elip có độ dài trục nhỏ bằng 8, hình chữ nhật cơ sở có chu vi bằng 40 là:
A. x 2 36 + y 2 16 = 1
B. 36 x 2 + 16 y 2 = 1
C. x 2 144 + y 2 64 = 1
D. 36 x 2 + 16 y 2 = 576
Ta có độ dài trục nhỏ bằng 8 nên 2b = 8 b = 4
Hình chữ nhật cơ sở có chu vi bằng 40 nên 4a + 4b = 40
Mà b = 4 nên a= 6
Phương trình chính tắc của (E): x 2 36 + y 2 16 = 1
Đáp án A
Đúng 0
Bình luận (0)
Viết phương trình hình chữ nhật cơ sở của Elip x2/1 + y2/2/3 = 1 Giúp mình với ạ