Một hình nón có đỉnh S có bán kính đáý bằng 2 a 3 , góc ở đỉnh là 120 ∘ . Thiết diện qua đỉnh của hình nón là 1 tam giác. Diện tích lớn nhất S m a x của tam giác là bao nhiêu?
![]()
![]()
![]()
![]()
Một hình nón có đỉnh S có bán kính đáý bằng 2 a 3 , góc ở đỉnh là 120 ° . Thiết diện qua đỉnh của hình nón là 1 tam giác. Diện tích lớn nhất S m a x của tam giác là bao nhiêu?
![]()
![]()
![]()
![]()
Một hình nón có đỉnh S có bán kính 2 a 3 góc ở đỉnh là 120°. Thiết diện qua đỉnh của hình nón là 1 tam giác. Diện tích lớn nhất S max của tam giác là bao nhiêu?
A. 8 a 2
B. 4 a 2 2
C. 4 a 2
D. 16 a 2
Cho hình nón đỉnh S có bán kính đáy R=a 2 , góc ở đỉnh bằng 60 0 . Diện tích xung quanh của hình nón bằng
![]()
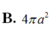
![]()
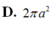
Cho hình nón đỉnh S, đáy là hình tròn tâm O, bán kính R=3cm, góc ở đỉnh hình nón là α = 120 ° . Cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A, B thuộc đường tròn đáy. Diện tích tam giác SAB bằng
A. 3 3 c m 2
B. 6 3 c m 2
C. 6 c m 2
D. 3 c m 2
Cho hình nón đỉnh S, đáy là hình tròn tâm O, bán kính R = 3cm, góc ở đỉnh hình nón là φ = 120 ° . Cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A, B thuộc đường tròn đáy. Diện tích tam giác SAB bằng:
A. 3 3 c m 2
B. 6 3 c m 2
C. 6 c m 2
D. 3 c m 2
Chọn đáp án A.
Góc ở đỉnh hình nón là φ = 120 ° là góc tạo bởi khi mặt phẳng đi qua trục SO => O S C ^ = 60 °
Khi cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB nên mặt phẳng không chứa trục của hình nón.
Xét tam giác vuông SOC tại O:
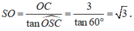
Xét tam giác vuông SOA tại O:
![]()
Do tam giác SAB đều:
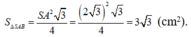
Cho mặt nón có góc ở đỉnh bằng 120 ° , thiết diện qua trục của hình nón N là một tam giác cân có bán kính đường tròn ngoại tiếp bằng 1. Tính chiều cao h của hình nón N .
A. h = 1 2
B. h = 3 2
C. h = 3 4
D. h = 1 4
Chọn đáp án A

Xét thiết diện qua trục của hình nón N là ∆ A B C cân tại A.
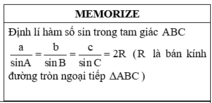
Theo định lí hàm số sin ta có
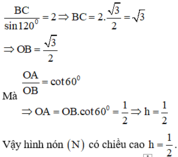
Cho hình nón có đỉnh S, đáy là hình tròn tâm O, bán kính R=3cm, góc ở đỉnh của hình nón là φ = 120 0 . Cắt hình nón bởi một mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A,B thuộc đường tròn đáy. Diện tích của tam giác SAB bằng
![]()
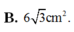
![]()
![]()
Cho hình nón có đỉnh S, đáy là hình tròn tâm O, bán kính R = 3 c m , góc ở đỉnh của hình nón là φ = 120 0. . Cắt hình nón bởi một mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A,B thuộc đường tròn đáy. Diện tích của tam giác SAB bằng
A. 3 3 c m 2 .
B. 6 3 c m 2 .
C. 6 c m 2 .
D. 3 c m 2 .
Cho hình nón đỉnh S có bán kính R = a 2 góc ở đỉnh bằng 60 độ Diện tích xung quanh của hình nón bằng
A. π a 2
B. 4 π a 2
C. 6 π a 2
D. 2 π a 2