Cho tam giác ABC vuông tại A có B = 38 độ , BC=8 cm . Hãy giải tam giác vuông ABC

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, BC=7, AC=6. Hãy giải tam giác vuông ABC?
Cho tam giác DEF vuông tại D, DE=7, Ê=40 độ. Hãy giải tam giác vuông DEF?
Bài 1:
Xét ΔABC vuông tại A có
\(AB^2+AC^2=BC^2\)
hay \(AB=\sqrt{13}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{6}{7}\)
nên \(\widehat{B}=59^0\)
hay \(\widehat{C}=31^0\)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A . Có AB bằng 6 cm. AC bằng 8 cm. a tính độ dài cạnh BC và chu vi tam giác ABC . Đường phân giác của góc B cắt AC tại D .Vẽ DH vuông góc BC . [ H thuộc BC ]. CM tam giác ABD = tam giác HBD c CM DA < DC . có vẽ hình nha mọi người
a: BC=10cm
C=AB+BC+AC=6+8+10=24(cm)
b: Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔABD=ΔHBD
c: Ta có: ΔABD=ΔHBD
nên DA=DH
mà DH<DC
nên DA<DC
Đúng 2
Bình luận (0)
Cho tam ABC vuông tại A có AB=6, AC=8. a, tính độ dài cạnh BC. b, đương qhan giác góc B cắt AC tại D vẽ DH vuông góc BC (H thuộc BC. Cm tam giác ABD=HBD. c, CM DA<D
(Tự vẽ hình)
a) Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
b) Xét \(\Delta ABD\) và \(\Delta HBD\) có:
\(\widehat{BAD}=\widehat{BHD}=90^0\)
\(BD\) chung
\(\widehat{ABD}=\widehat{HBD}\) (tính chất phân giác)
\(\Rightarrow\Delta ABD=\Delta HBD\) (ch - gn)
c) Ta có \(\Delta ABD=\Delta HBD\Rightarrow AD=HD\)
Mà \(HD< DC\) (do \(\Delta HDC\) vuông tại \(H\))
\(\Rightarrow DA< DC\)
Đúng 0
Bình luận (0)
a, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AC^2+AB^2}=10cm\)
b, Xét tam giác BAD và tam giác BHD có
BD _ chung ; ^ABD = ^HBD ; ^BAD = ^BHD = 900
Vậy tam giác BAD = tam giác BHD ( ch-gn)
Đúng 0
Bình luận (0)
Bài 1: Cho một tam giác vuông có độ dài hai cạnh góc vuông tỉ lệ 6:8. Biết cạnh huyền dài 55 cm. Hãy tính độ dài hai cạnh góc vuông
Bài 2: Cho tam giác vuông ABC đường vuông góc hạ từ A xuống BC là AH. Biết AH= 6 cm, BH= 4,5 cm, HC= 8 cm.Hỏi tam giác ABC là tam giác gì?.
Cho tam giác ABC vuông tại A, AC = 8 cm, AB = 6 cm và tam giác HIK vuông tại H, HI = 15 cm, IK = 25 cm
a) Tính độ dài BC, HK
b) Hai tam giác ABC và HIK có đồng dạng vs nhau k? Vì sao?
điểm H,K,I ở chỗ nào vậy
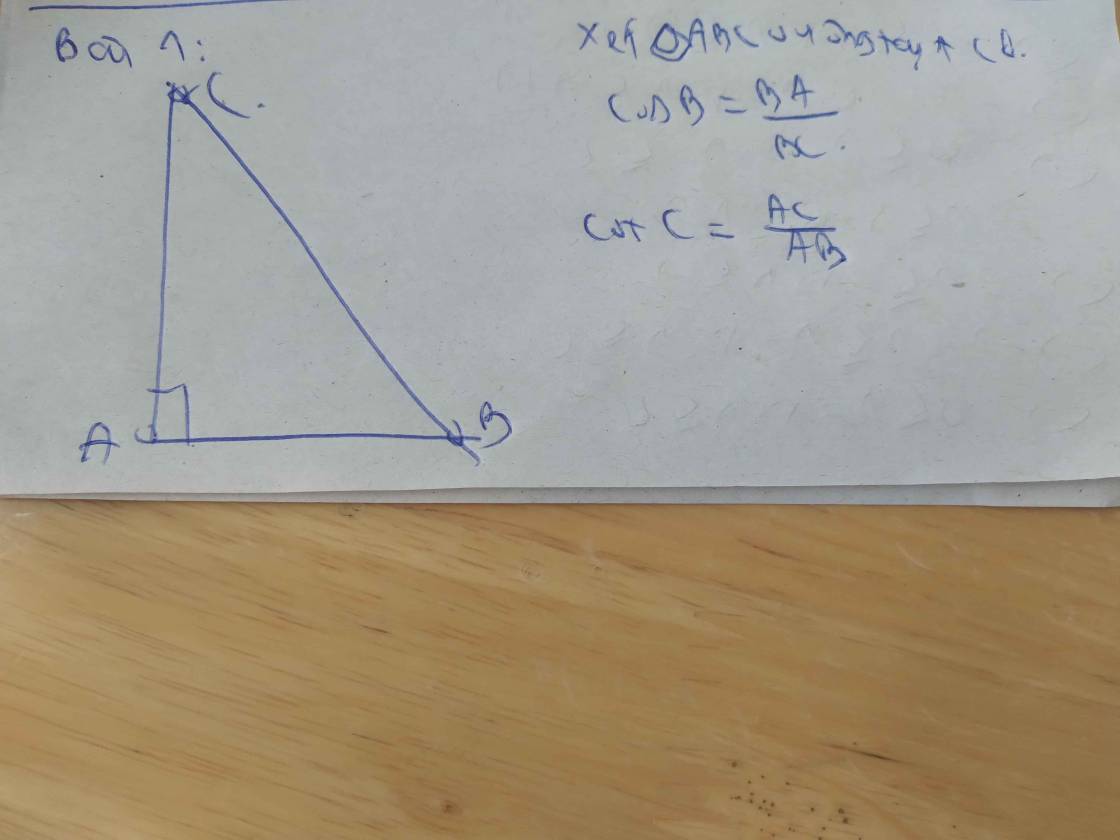
Bài 1 : Cho tam giác ABC vuông tại A hãy viết tỉ số lượng giác CosB và cotC Bài 2 :. Cho tam giác ABC vuông tại A có đường cao AK chia cạnh huyền BC thành hai đoạn KB=3 cm và KC=9 cm a) Tỉnh độ dài các đoạn thẳng: BC,AB b) Tính độ dài đoạn thẳng AK c) Trên cạnh AC lấy điểm M ( M khác A và C ). Gọi H là hình chiếu cùa A trên BM. Chứng minh rằng BH .BM=BK . BC
Cho tam giác ABC vuông tại A, biết , BC = 10 cm .
a)Giải tam giác vuông ABC ?
b)Vẽ đường cao AH, đường trung tuyến AM . Tính độ dài AH, HM?
a, \(\tan B=\dfrac{4}{3}\Leftrightarrow\dfrac{AC}{AB}=\dfrac{4}{3}\Leftrightarrow AC=\dfrac{4}{3}AB\)
Áp dụng PTG: \(AB^2+AC^2=AB^2+\dfrac{16}{9}AB^2=\dfrac{25}{9}AB^2=BC^2=100\)
\(\Leftrightarrow AB^2=36\Leftrightarrow AB=6\left(cm\right)\\ \Leftrightarrow AC=6\cdot\dfrac{4}{3}=8\left(cm\right)\)
\(\tan B=\dfrac{4}{3}\approx\tan53^0\Leftrightarrow\widehat{B}\approx53^0\\ \widehat{C}=90^0-\widehat{B}\approx90^0-53^0=37^0\)
b, Vì AM là trung tuyến ứng ch BC nên \(AM=\dfrac{1}{2}BC=5\left(cm\right)\)
Áp dụng HTL: \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{48}{10}=4,8\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC, vuông tại B có B = 60 độ, AB = 5cm, BC = 10cm. Tia phân giác của B cắt AC tại D. Kẻ DE vuông góc BC tại E
a/ Cm: tam giác ABC = EBD
b/ Cm: tam giác ABE là tam giác đều
c/ Tính độ dài cạch AC
giúp mik vs!
chịu................................................................................ ko hiểu
Mình cần gấp ạ....
1)Cho tam giác ABC cân tại A có AB=6 cm,BC=4 cm.Tính các góc trong tam giác ABC.
2)Cho tam giác ABC vuông tại A có góc B=50 độ,BC=5 cm.Ở phía ngoài tam giác ABC,vẽ tam giác vuông ADC có góc CAD=35 độ.Tính chu vi tam giác ABC và chu vi tam giác ADC