Cho hình vẽ chứng minh tứ giác ABCD là hình bình hành.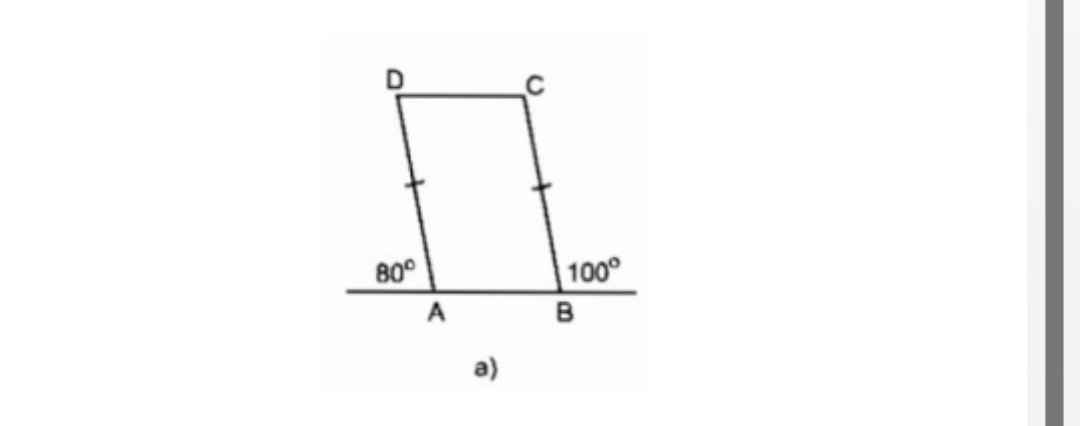

Những câu hỏi liên quan
Cho tứ giác ABCD. Vẽ các hình bình hành ABID, ACJD. Chứng minh tứ giác BIJC là hình bình hành
ta có hbh ABID => AD=BI; AD//BI
ta có hbh ACJD=> AD//CJ; AD=CJ
=> BI//CJ( // AD); BI=CJ (=AD)
=> BICJ là hbh
Đúng 1
Bình luận (1)
Cho hình bình hành ABCD. Ở miền trong hình bình hành ABCD vẽ hình bình hành A'B'C'D'. Gọi M, N, P, Q lần lượt là trung điểm của AA', BB', CC', DD'. Chứng minh rằng tứ giác MNPQ là hình bình hành
Lấy E là trung điểm A'D ; F là trung điểm BC'.
Dễ dàng chứng minh được \(\Delta EQM=\Delta FNP\left(c.g.c\right)\)
Từ đó suy ra \(MQ=NP\)
CMTT có \(MN=PQ\)
Do đó \(MNPQ\)là hình bình hành.
Vậy ...
Đúng 0
Bình luận (0)
Câu IV. a. Tính số đo góc E của tứ giác EFGH trong hình vẽ bên. b. Cho hình bình hành ABCD. Gọi E là trung điểm AD, F là trung điểm BC. Chứng minh tứ giác EBFD là hình bình hành
b: Xét tứ giác EBFD có
ED//BF
ED=BF
Do đó: EBFD là hình bình hành
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD, Trên cạnh AB lấy điểm M, trên cạnh CD lấy điểm N sao cho a, Chứng minh rằng: . b, Chứng minh tứ giác AMCN là hình bình hành. c, Chứng minh tứ giác BMDN là hình bình hành
Đọc tiếp
Cho hình bình hành ABCD, Trên cạnh AB lấy điểm M, trên cạnh CD lấy điểm N sao cho ![]()
a, Chứng minh rằng: ![]() .
.
b, Chứng minh tứ giác AMCN là hình bình hành.
c, Chứng minh tứ giác BMDN là hình bình hành
Cho hình bình hành ABCD. Vẽ AM ^ BD tại M, AM cắt CD ở E. Vẽ CN ^ BD tại N, CN cắt AB ở F.
Chứng minh rằng :
a) Tứ giác AECF là hình bình hành
b) Tứ giác AMCN là hình bình hành
a) xét tg AECF có : AF//EC (vì AB//CD, tgABCD là hbh)
và AE//CF ( cùng ^ vsBD)
=> tgAECF là hbh
b)xét tg AMD và tg CNB có:
AD=BC (tgABCD là hbh)
AMD =CNB =90
ADM =CBN (AD//BC)
=>tg AMD =tg CNB (ch-gn)
=>AM=CN (2 cạnh t/ư )
xét tg AMCN có: AM//CN (do cùng ^ BD) và AM =CN (cmt)
==>tg AMCN là hbh
Đúng 2
Bình luận (0)
Cho hình bình hành ABCD. Vẽ AM vuong goc BD tại M, AM cắt CD ở E. Vẽ CN vuong goc BD tại N, CN cắt AB ở F. Chứng minh rằng : a) Tứ giác AECF là hình bình hành b) Tứ giác AMCN là hình bình hành
mk cần phần b thôi
Cho hình bình hành ABCD có AB<AD . Tia phân giác của B, D lần lượt cắt AD, BC tại M, N
a) ΔABM là tam giác gì?
b) Chứng minh tứ giác BMDN là hình bình hành
(vẽ hình giúp mình)
a: góc ABM=góc MBC
góc MBC=góc AMB
=>góc ABM=góc AMB
=>ΔABM cân tại A
b: Xét ΔBAM và ΔDCN có
góc ABM=góc CDN
BA=DC
góc A=góc C
Do đó: ΔBAM=ΔDCN
=>AM=CN
AM+MD=AD
BN+NC=BC
mà AD=BC và AM=CN
nên MD=BN
Xét tứ giác MDNB có
MD//NB
MD=NB
Do đó: MDNB là hình bình hành
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD . Trên cạnh AB lấy điểm E , trên cạnh CD lấy điểm F sao cho AE = CF. a / Chứng minh DE = BF b / Chứng minh tứ giác AECF là hình bình hành . c / Chứng minh tứ giác BEDF là hình bình hành
a: Ta có: AE+EB=AB
DF+FC=DC
mà AE=FC
và AB=DC
nên EB=DF
Xét tứ giác EBFD có
EB//DF
EB=DF
Do đó: EBFD là hình bình hành
Suy ra: DE=BF
b: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Đúng 1
Bình luận (0)
Cho hình bình hành ABCD có AB = 2AD. Gọi M,N lần lượt là trung điểm của AB,CD
a) chứng minh tứ giác ABCD là hình bình hành
b)chừng minh tứ giác AMND là hình thoi
c)Gọi K là điểm đối xứng vời điểm A qua D.Gọi Q là điểm đối xứng với N qua D.Tứ giác ANKQ là hình gì? Vì sao?
d)Hình bình hành ABCD có thêm điều kiện gì để tứ giác ABCN là hình thang cân
(nhớ vẽ hình nha)
Bài làm:
a, hbh ABCD có: AB // CD và AB = CD
=> AM // DN và AM = DN
=> AMND là hbh mà AB = 2AD => 1/2AB = AD => AM = AD
=> AMND là hthoi
b, cmtt câu a ta có: MB // ND và MB = ND
=> MBND là hbh


















