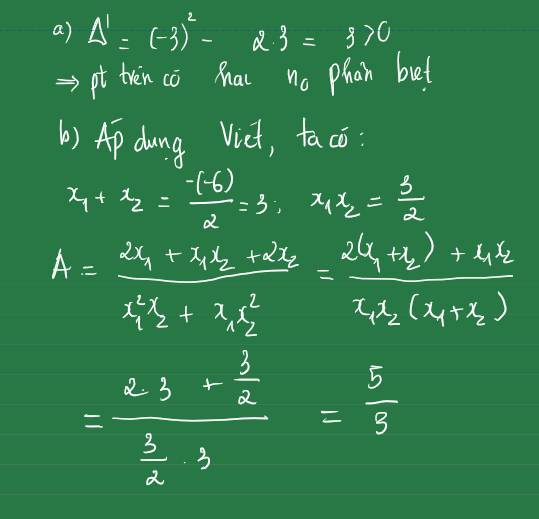chứng tỏ bất phương trình: x2-2x+17<3-4x vô nghiệm
Giúp mình với ạ!
Những câu hỏi liên quan
chứng tỏ bất phương trình : x2 - 2x + 17< 3 - 4x vô nghiệm?
tham khảo câu hỏi của đắng sôcôla trên hoc24.vn nha
Đúng 0
Bình luận (0)
Cho bất phương trình x2 > 0.
a) Chứng tỏ x = 2, x = -3 là nghiệm của bất phương trình đã cho.
b) Có phải mọi giá trị của ẩn x đều là nghiệm của bất phương trình đã cho hay không?
a) Thay x = 2 vào bất phương trình ta được: x2 = 22 = 4 > 0
Vậy x = 2 là một nghiệm của bất phương trình x2 > 0.
Thay x = -3 vào bất phương trình ta được x2 = (-3)2 = 9 > 0
Vậy x = -3 là một nghiệm của bất phương trình x2 > 0.
b) Với x = 0 ta có x2 = 02 = 0
⇒ x = 0 không phải nghiệm của bất phương trình x2 > 0.
Vậy không phải mọi giá trị của ẩn x đều là nghiệm của bất phương trình đã cho.
Đúng 0
Bình luận (0)
Chứng minh bất phương trình sau vô nghiệm:
1
+
2
x
-
3
2
+
5
-
4
x
+
...
Đọc tiếp
Chứng minh bất phương trình sau vô nghiệm: 1 + 2 x - 3 2 + 5 - 4 x + x 2 < 3 2
Tập xác định: D = R.
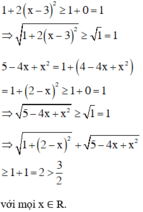
Do đó BPT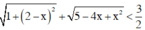 
vô nghiệm.
Đúng 0
Bình luận (0)
Chứng tỏ các số 3; 4 và 5 đều là nghiệm, còn số 6 không phải là nghiệm của bất phương trình x2 ≤ 6x –5
+ Với x = 3, BPT trở thành 32 ≤ 6.3 –5 hay 9 ≤ 13 (đúng)
Do đó x = 3 là nghiệm của bất phương trình.
+ Với x = 4, BPT trở thành: 42 ≤ 6.4 –5 hay 16 ≤ 19 (Đúng)
Do đó x = 4 là nghiệm của bất phương trình.
+ Với x = 5, BPT trở thành 52 ≤ 6.5 –5 hay 25 ≤ 25 (Đúng)
Do đó x = 5 là nghiệm của bất phương trình
+ Với x = 6 , BPT trở thành: 62 ≤ 6.6 –5 hay 36 ≤ 31 (Sai)
Do đó x = 6 không là nghiệm của bất phương trình.
Đúng 0
Bình luận (0)
Chứng tỏ các phương trình sau vô nghiệm:
a. |x|+1=0 b. x2 + 2x + 3=0
a) Ta có \(\left|x\right|\ge0\) nên |x| + 1 > 0 với mọi x. Do đó phương trình đã cho vô nghiệm.
b) Tương tự, phân tích \(x^2+2x+3=\left(x+1\right)^2+2>0\)
Đúng 4
Bình luận (0)
Cho phương trình 2x^2 - 6x +3 =0
a) chứng tỏ phương trình trên có 2 nghiệm phân biệt x1 x2
b) Không giải phương trình để tìm 2 nghiệm x1, x2, hãy tính giá trị của biểu thưc A= 2x1 +x1.x2 +2x2 phần x12 .x2 +x1.x22
Chứng tỏ rằng các phương trình sau vô nghiệm:
a.x2+2x+3/x2-x+1=0
b.x/x+2+4/x-2=4/x2-4
a. \(\dfrac{x^2+2x+3}{x^2-x+1}=0\) ⇔x2+2x+3=0 ⇔x2+2x+1+2=0 ⇔(x+1)2+2=0
Vì (x+1)2+2>0 nên phương trình đã cho vô nghiệm.
b) \(\dfrac{x}{x+2}+\dfrac{4}{x-2}=\dfrac{4}{x^2-4}\) ⇔\(\dfrac{x\left(x-2\right)+4\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{4}{\left(x-2\right)\left(x+2\right)}\)
⇔\(x\left(x-2\right)+4\left(x+2\right)=4\) ⇔x2-2x+4x+8-4=0 ⇔x2+2x+4=0 ⇔x2+2x+1+3=0 ⇔(x+1)2+3=0
Vì (x+1)2+3>0 nên phương trình đã cho vô nghiệm.
Đúng 1
Bình luận (0)
CM các bất phương trình sau luôn dương vs mọi x
1)2x2-2x+17>0
2)-x2+6x-18<0
3)|x-1|+|x|+2>1
BPT thì làm sao gọi là luôn dương hả bạn? Đề phải là CMR các BPT sau luôn đúng với mọi $x$.
1.
Ta có: $2x^2-2x+17=x^2+(x^2-2x+1)+16=x^2+(x-1)^2+16\geq 16>0$ với mọi $x\in\mathbb{R}$
Do đó BPT luôn đúng với mọi $x$
2.
$-x^2+6x-18=-(x^2-6x+18)=-[(x^2-6x+9)+9]=-[(x-3)^2+9]$
$=-9-(x-3)^2\leq -9<0$ với mọi $x\in\mathbb{R}$
Vậy BPT luôn đúng với mọi $x$
3.
$|x-1|+|x|+2\geq 0+0+2=2>1$ với mọi $x\in\mathbb{R}$
Do đó BPT luôn đúng với mọi $x$
Đúng 0
Bình luận (0)
5 tháng 2 2021 lúc 14:52
chứng tỏ rằng các phương trình sau đây vô nghiệm :
a)2(x+1)=2x-1 b)x2+4x+5=0
c)4x2+2x+1=0 d)x2-x+1=0
a) 2(x+1)=2x-1
<=> 2x+2=2x-1
<=> 2x+2-2x+1=0
<=>1=0
=>Pt vô nghiệm
Đúng 0
Bình luận (0)
Chứng tỏ rằng phương trình 3 x 2 +2x -21 =0 có một nghiệm là -3.Hãy tìm nghiệm kia
Thay x =-3 vào vế trái của phương trình , ta có:
3. - 3 2 +2(-3) -21 =27 – 6 -21 =0
Vậy x = -3 là nghiệm của phương trình 3 x 2 +2x -21 =0
Theo hệ thức vi-ét ta có : x 1 x 2 = c/a = -21/3 = -7 ⇒ x 2 = -7/ x 1 = -7/-3 = 7/3
Vậy nghiệm còn lại là x = 7/3
Đúng 0
Bình luận (0)