\(B=\dfrac{2^{15}\cdot5^8-2^5\cdot2^9\cdot5^9}{2^{16}\cdot5^7+2^{16}\cdot5^8}=\dfrac{2^{14}\cdot5^8\cdot\left(2-5\right)}{2^{16}\cdot5^7\left(1+5\right)}=\dfrac{1}{4}\cdot5\cdot\dfrac{-1}{2}=\dfrac{-5}{8}\)

Rút gọn:

\(a,B=4\sqrt{x=1}-3\sqrt{x+1}+2\)\(\sqrt{x+1}+\sqrt{x+1}\)

\(=4\sqrt{x+1}\)

\(b,\)đưa về \(\sqrt{x+1}=4\Rightarrow x=15\)

a, Với \(x\ge-1\)

\(\Rightarrow B=4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}\)

\(=4\sqrt{x+1}\)

b, Ta có B = 16 hay 

\(4\sqrt{x+1}=16\Leftrightarrow\sqrt{x+1}=4\)bình phương 2 vế ta được 

\(\Leftrightarrow x+1=16\Leftrightarrow x=15\)

a) B = 4√x+1                                   b) x = 15

a) Rút gọn:

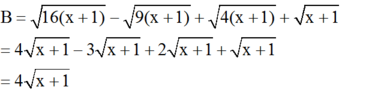
b) Để B = 16 thì:

⇔ x + 1 = 16 ⇔ x = 15 (thỏa mãn x ≥ -1)

\(=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)+2\sqrt{x}\left(\sqrt{x}+3\right)-3x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{x-9}=\dfrac{3\sqrt{x}-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{3}{\sqrt{x}+3}\)

\(A=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\) (ĐK: \(x\ge0;x\ne9\))

\(A=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{\left(\sqrt{x}\right)^2-3^2}\)

\(A=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{3x+9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

\(A=\dfrac{x-3\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\dfrac{2x+6\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{3x+9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

\(A=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

\(A=\dfrac{3\sqrt{x}-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

\(A=\dfrac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)

\(A=\dfrac{3}{\sqrt{x}+3}\)

A = \(\dfrac{3}{\sqrt{x}+3}\)

a.

\(B=\sqrt{16x+16}-\sqrt{9x+9}+\sqrt{4x+4}+\sqrt{x+1}\left(x\ge-1\right)\)

\(B=\sqrt{16}.\sqrt{x+1}-\sqrt{9}.\sqrt{x+1}+\sqrt{4}.\sqrt{x+1}+\sqrt{x+1}\)

\(B=4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}\)

\(B=\left(4-3+2+1\right).\sqrt{x+1}\)

\(B=4.\sqrt{x+1}\)

b.

\(B=16\\\)

\(\Rightarrow4\sqrt{x+1}=16\)

\(\Rightarrow\sqrt{x+1}=\dfrac{16}{4}=4\)

\(\Rightarrow x+1=4^2\)

\(\Rightarrow x+1=16\rightarrow x=16-1=15\) (thỏa mãn)

vậy x=15

a: Thay x=16 vào A, ta được:

\(A=\dfrac{2\cdot4}{4+3}=\dfrac{8}{7}\)

a, \(=\frac{8\left(x+2y\right)^5}{2\left(x+2y\right)}=8\left(x+2y\right)^4\)

b,\(=\left(\frac{3}{4}\right)^{45}:\left(\left(\frac{3}{4}\right)^2\right)^{10}\)

\(=\left(\frac{3}{4}\right)^{45}:\left(\frac{3}{4}\right)^{2.10}=\left(\frac{3}{4}\right)^{25}\)

thiếu nè 8:2=4 nha sửa lại cái