Tìm các số hữu tỉ a,b biết:
\(a+\frac{b}{2}=\frac{ab}{2}=8.\frac{a}{b}\)
bài 1:
tìm 2 số hữu tỉ a và b biết a+b=a nhân b=a/b
bài2
tìm 2 số nguyên x và y biết:
\(\frac{5}{x}+\frac{y}{4}=\frac{1}{8}\)
Bài 1: Ta có:
a + b = a.b => a = a.b - b = b.(a - 1) (1)
=> a : b = a - 1 = a + b
=> b = -1
Thay b = -1 vào (1) ta có: a = -1.(a - 1) = -a + 1
=> a + a = 1 = 2a
\(\Rightarrow a=\frac{1}{2}\)
Vậy \(a=\frac{1}{2};b=-1\)
b) \(\frac{5}{x}+\frac{y}{4}=\frac{1}{8}\)
\(\Rightarrow\frac{5}{x}=\frac{1}{8}-\frac{y}{4}=\frac{1-2y}{8}\)
=> (1 - 2y).x = 40
\(\Rightarrow40⋮1-2y\)
Mà 1 - 2y là số lẻ \(\Rightarrow1-2y\in\left\{1;-1;5;-5\right\}\)
Ta có bảng sau:
| 1 - 2y | 1 | -1 | 5 | -5 |
| x | 40 | -40 | 8 | -8 |
| y | 0 | 1 | -2 | 3 |
Vậy các cặp giá trị (x;y) thỏa mãn đề bài là: (40;0) ; (-40;1) ; (8;-2) ; (-8;3)
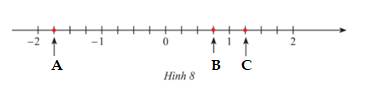
a) Các điểm A,B,C trong Hình 8 biểu diễn số hữu tỉ nào?
b) Biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số.
a) Các điểm A,B,C trong Hình 8 biểu diễn lần lượt các số hữu tỉ: \(\frac{{ - 7}}{4};\,\frac{3}{4};\,\frac{5}{4}.\)
b) Ta có: \(1\frac{1}{5} = \frac{6}{5};\,\,\, - 0,8 = \frac{{ - 8}}{{10}} = \frac{{ - 4}}{5}.\)
Vậy ta biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số như sau:

a) tìm a,b,c là các số hữu tỉ biết : \(a+b=\frac{5}{2};b+c=\frac{9}{4};c+a=-\frac{5}{4}\)
b)tìm a,b,c_____________biết :\(ab=-6;bc=-15;ac=10\)
2(a+b+c)=\(\frac{5}{2}+\frac{9}{4}+\frac{-5}{4}=3\frac{1}{2}\)
suy ra a+b+c\(=3\frac{1}{2}:2=1\frac{3}{4}\)
suy ra c\(=1\frac{3}{4}-\frac{5}{2}=\frac{-3}{4}\)
suy ra a\(=1\frac{3}{4}-\frac{9}{4}=\frac{-1}{2}\)
suy ra b\(=1\frac{3}{4}-\frac{-5}{4}=3\)
cho a,b,c là các số hữu tỉ thỏa mãn:abc=1 và \(\frac{a}{b^2}+\frac{b}{c^2}+\frac{c}{a^2}=\frac{b^2}{a}+\frac{c^2}{b}+\frac{a^2}{c}\) tìm a,b,c
\({ x^3\over x^4-1 }={{ a(x+1)+b(x-1)}\over{x^2-1}} +{{cx+d}\over{x^2+1}}\)=\({(ax+a+bx-b)(x^2 +1) +(cx+d) (x^2-1)}\over{x^4-1}\) =\({ax^3 +ax^2+bx^3-bx^2+ax+a+bx-b +cx^3 +dx^2-cx-d}\over{x^4-1} \) Suy ra \(x^3=ax^3 +ax^2+bx^3-bx^2+ax+a+bx-b +cx^3 +dx^2-cx-d \) \(= x^3(a+b+c)+x^2(a-b+d)+x(a+b-c)+(a-b-d)\) Điều này chỉ xảy ra khi đồng thời : a+b+c=1; a-b+d=0; a+b-c=0; a-b-d=0 khi và chỉ khi a=0,25 ; b=0,25 ; c=0,5 ; d=0
Vậy .......
Biến đổi đẳng thức về dạng :
\(\frac{x^3}{x^4-1}=\frac{\left(a+b+c\right).x^3+\left(a-b+d\right).x^2+\left(a+b-c\right).x+\left(a-b-d\right)}{x^4-1}\)
Suy ra \(\hept{\begin{cases}a+b+c=1\\a-b+d=0\\a+b-c=0\end{cases}}\)Giải ra ta được a=b=1/4 ; c = 1/2 ; d = 0
\(\hept{a-b-d=0}\)
( Lưu ý : Phần lưu ý này không cần phải ghi : Nối dấu ngoặc 3 ý và dấu ngoặc 1 ý làm 1 )
cho dãy số hữu tỉ:
\(\frac{2}{3};\frac{4}{5};\frac{7}{8};\frac{3}{4};\frac{9}{10};\frac{8}{9};\frac{5}{6};\frac{6}{7}\)
a)Sắp xếp các số hữu tỉ theo thứ tự tăng dần
Nếu\(\frac{a}{b}\)là một số thuộc dãy trên thì số tiếp theo là số nào?
b)So sánh \(\frac{a}{b}\)với\(\frac{a+1}{a+2}\)
\(a)\)
Ta có :
\(1-\frac{2}{3}=\frac{1}{3};1-\frac{4}{5}=\frac{1}{5};1-\frac{7}{8}=\frac{1}{8};1-\frac{3}{4}=\frac{1}{4}\)
\(1-\frac{9}{10}=\frac{1}{10};1-\frac{8}{9}=\frac{1}{9};1-\frac{5}{6}=\frac{1}{6};1-\frac{6}{7}=\frac{1}{7}\)
Do \(\frac{1}{3}>\frac{1}{4}>\frac{1}{5}>\frac{1}{6}>\frac{1}{7}>\frac{1}{8}>\frac{1}{9}>\frac{1}{10}\)
\(\Rightarrow1-\frac{1}{3}< 1-\frac{1}{4}< 1-\frac{1}{5}< 1-\frac{1}{6}< 1-\frac{1}{7}< 1-\frac{1}{8}< 1-\frac{1}{9}< 1-\frac{1}{10}\)
\(\Rightarrow\frac{2}{3}< \frac{3}{4}< \frac{4}{5}< \frac{5}{6}< \frac{6}{7}< \frac{7}{8}< \frac{8}{9}< \frac{9}{10}\)
Nếu \(\frac{a}{b}\)là 1 số thuộc dãy trên thì số tiếp theo là :
\(\frac{a+1}{b+1}\)
\(b)\)
Ta có :
\(a\left(a+2\right)=a^2+2a\)
\(b\left(a+1\right)=ab+b\)
Sorry , đến bước này mik chịu
~ Ủng hộ nhé
Phần b) Ý bạn là so sánh \(\frac{a}{b}\)và \(\frac{a+1}{b+2}\)
cho a,b là các số hữu tỉ thỏa mãn \(a^2+b^2=4-\left(\frac{ab+2}{a+b}\right)^2\).CMR:\(\sqrt{ab+2}\)là số hữu tỉ
cho a,b,c là số hữu tỉ ,a=b+c
cm a) \(\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}\) là số hữu tỉ
b) \(\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{\left(a+b\right)^2}}\) là số hữu tỉ
a/ \(\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}=\sqrt{\frac{1}{\left(b+c\right)^2}+\frac{1}{b^2}+\frac{1}{c^2}}\)
\(=\sqrt{\frac{\left(b+c\right)^2.b^2+\left(b+c\right)^2.c^2+b^2.c^2}{\left(b+c\right)^2.b^2.c^2}}\)
\(=\sqrt{\frac{\left(b^2+bc+c^2\right)^2}{\left(b+c\right)^2.b^2.c^2}}\)
\(=\left|\dfrac{b^2+bc+c^2}{\left(b+c\right).b.c}\right|\)
Vậy \(\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}\)là số hữu tỉ
b/ \(\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{\left(a+b\right)^2}}=\sqrt{\frac{1}{\left(b+c\right)^2}+\frac{1}{b^2}+\frac{1}{\left(2b+c\right)^2}}\)
\(=\sqrt{\frac{\left(b+c\right)^2.b^2+\left(b+c\right)^2.\left(2b+c\right)^2+\left(2b+c\right)^2.b^2}{\left(b+c\right)^2.\left(2b+c\right)^2.b^2}}\)
\(=\sqrt{\frac{\left(3b^2+3bc+c^2\right)^2}{\left(b+c\right)^2.\left(2b+c\right)^2.b^2}}\)
\(=\left|\dfrac{3b^2+3bc+c^2}{\left(b+c\right).\left(2b+c\right).b}\right|\)
Vậy \(\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{\left(a+b\right)^2}}\) là số hữu tỉ
Cho a,b,c là các số hữu tỉ chứng minh rằng: \(\sqrt{\frac{1}{\left(a-b\right)^2}+\frac{1}{\left(b-c\right)^2}+\frac{1}{\left(c-a\right)^2}}\)là số hữu tỉ
bạn tham khảo nhé : https://olm.vn/hoi-dap/detail/106812735697.html
không hiện link thì mình gửi qua tin nhắn nhé