Tìm nghiệm nguyên của phương trình
4y4+6y2-1=x
Những câu hỏi liên quan
Giải phương trình nghiệm nguyên:
6y2 = x(x+1)(2x+1)
Thu gọn đa thức ta được: x3 – 5y2 + x + x3 – y2 – x ta được
(A) x6 - 6y4;
(B) x6 - 4y4;
(C) 2x3 - 6y2;
(D) 2x3 - 4y2.
Hãy chọn phương án đúng
x3 – 5y2 + x + x3 – y2 – x
= (x3 + x3) – (5y2 + y2) + (x – x)
= (1+ 1).x3 – (5+1).y2 + (1- 1).x
= 2x3 – 6y2
Đáp án đúng là (C) 2x3 - 6y2
Đúng 0
Bình luận (0)
Cho hệ phương trình
y
2
-
2
x
+
3
0
5
x
2
-
7
x...
Đọc tiếp
Cho hệ phương trình y 2 - 2 x + 3 = 0 5 x 2 - 7 x y - 6 y 2 = 0 .Giả sử (x;y) là nghiệm của hệ phương trình. Giá trị nhỏ nhất của x 2 + y 2 là:
A. 45
B. 9
C. 2
D. 5
Hệ phương trình
x
2
+
y
6
y
2
+
x
6
có bao nhiêu nghiệm? A. 6 B. 4 C. 2 D. 0
Đọc tiếp
Hệ phương trình x 2 + y = 6 y 2 + x = 6 có bao nhiêu nghiệm?
A. 6
B. 4
C. 2
D. 0
Hệ phương trình
x
2
+
y
6
y
2
+
x
6
có bao nhiêu nghiệm: A. 6 B. 4 C. 2 D. 0
Đọc tiếp
Hệ phương trình x 2 + y = 6 y 2 + x = 6 có bao nhiêu nghiệm:
A. 6
B. 4
C. 2
D. 0
Đáp án B
Trừ vế với vế của phương trình ta được:
Đúng 0
Bình luận (0)
Hệ phương trình
x
2
+
y
6
y
2
+
x
6
có bao nhiêu nghiệm? A. 6 B. 4 C. 2 D. 0
Đọc tiếp
Hệ phương trình x 2 + y = 6 y 2 + x = 6 có bao nhiêu nghiệm?
A. 6
B. 4
C. 2
D. 0
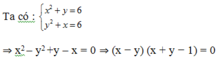
- Khi x = y thì x 2 + x - 6 = 0 ⇔ x = - 3 ; x = 2
- Khi y = 1 - x thì x 2 + 1 - x - 6 = 0 ⇔ x 2 - x - 5 = 0 ⇔ x 1 , 2 = 1 ± 21 2
Vậy hệ phương trình đã cho có 4 nghiệm (−3; −3), (2; 2), 1 + 21 2 ; 1 − 21 2 và 1 − 21 2 ; 1 + 21 2
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
1. tìm nghiệm nguyên của phương trình:
p(x + y) = xy và p nguyên tố
2. tìm nghiệm nguyên của phương trình:
a. x + y + z + 9 = xyz
b. x + y + 1 = xyz
1. Tìm nghiệm nguyên của phương trình : x^2 + ( x+ 1)^2 = y^4 + (y+1)^4
2.tìm ngiệm nguyên của phương trình : x^2 - 3y^2 =17
cho phương trình:
mx - 3 = 2x =2m
1) tìm m để phương trình vô nghiệm, phương trình có nghiệm
2) khi phương trình có nghiệm duy nhất :
a) tìm m nguyên để phương trình có nghiệm nguyên
b) tìm m để phương trình có nghiệm x>0
c) tìm m để phương trình có nghiệm x<0
1)Tìm nghiệm nguyên của phương trình:
y3-x3=91
2)Tìm nghiệm nguyên của phương trình:
x2=y2+y+13
3)Tìm nghiệm nguyên của phương trình:
x2+x+1991=y2