1,Cho A=x/y+1 +y/x+1 bới x>0;y>0 và x+y=1
tìm GTNN,GTLN của A
2,Cho a+b+c=3 và a,b,c >0
Chứng minh \(\frac{a^2}{1+b}+\frac{b^2}{1+c}+\frac{c^2}{1+a}\ge\frac{3}{2}\)
Cho hình phẳng (H) giới hạn bới các đường y = 3 x + 1 , y = x - 1 và x = 1 . Diện tích S của hình phẳng (H) là
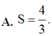
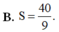
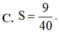
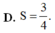
Cho hình phẳng (H) giới hạn bới các đường y = 3 x + 1 , y = x - 1 và x = 1 . Diện tích S của hình phẳng (H) là
A. S = 4 3 .
B. S = 40 9 .
C. S = 9 40 .
D. S = 3 4 .
Cho x,y,z>0 và x+y+z=1 . Tìm MinP = ∑ \(\dfrac{1}{x+y+1}\)
Cho x,y,z>0 và x+y+z =1 . Tìm Min A = ∑ \(\dfrac{x}{y^2+x^2+1}\)
\(P=\sum\dfrac{1}{x+y+1}\ge\dfrac{9}{2\left(x+y+z\right)+3}=\dfrac{9}{2.1+3}=\dfrac{9}{5}\)
Dấu \("="\Leftrightarrow x=y=z=\dfrac{1}{3}\)
1. Cho x2 +y2 =1. Tìm min A= (3-x) (3-y).
2. cho x,y >0, 2xy-4= x+y. Tìm min P=xy+ 1/ x2 +1/ y^2.
3.Cho x>=3, y>= 3. Tìm min A= 21*(x+1/y) +3*(y+1/x).
4. Cho x,y >0, x^2+ y^2= 1.Tìm min x+y+1/x+1/y.
5. Cho a,b>0, a+b+3ab=1. Tìm min A= 6ab/ (a+b) -a^2-b^2
a, Cho `0<x<25`
Tìm GTLN:`(80-2x)(50-2x)x`
b, `0<x<2`. Tìm GTLN: `5x(2-x)`
c, `x≥2`. Tìm GTLN: `x + 1/x`
d, Cho `x,y>0, x+y≤1`. TÌm GTNN: `x + y + 1/x + 1/y`
d. Áp dụng BĐT Caushy Schwartz ta có:
\(x+y+\dfrac{1}{x}+\dfrac{1}{y}\le x+y+\dfrac{\left(1+1\right)^2}{x+y}=x+y+\dfrac{4}{x+y}\le1+\dfrac{4}{1}=5\)
-Dấu bằng xảy ra \(\Leftrightarrow x=y=\dfrac{1}{2}\)
c. Bạn kiểm tra lại đề nhé.
b. \(5x\left(2-x\right)=-5x\left(x-2\right)=-5\left(x^2-2x\right)=-5\left(x^2-2x+1-1\right)=-5\left(x-1\right)^2+5\le5\)-Dấu bằng xảy ra \(\Leftrightarrow x=1\)
a.
\(\left(80-2x\right)\left(50-2x\right)x=\dfrac{2}{3}\left(40-x\right)\left(50-2x\right)3x\le\dfrac{2}{3}\left(\dfrac{40-x+50-2x+3x}{3}\right)^3=18000\)
Dấu "=" xảy ra khi \(40-x=50-2x=3x\Leftrightarrow x=10\)
b.
\(5x\left(2-x\right)=5.x\left(2-x\right)\le\dfrac{5}{4}\left(x+2-x\right)^2=5\)
Dấu "=" xảy ra khi \(x=2-x\Rightarrow x=1\)
c.
Biểu thức này chỉ có min, ko có max
d.
\(x+y\le1\Rightarrow-\left(x+y\right)\ge-1\)
\(x+y+\dfrac{1}{x}+\dfrac{1}{y}=\left(4x+\dfrac{1}{x}\right)+\left(4y+\dfrac{1}{y}\right)-3\left(x+y\right)\ge2\sqrt{\dfrac{4x}{x}}+2\sqrt{\dfrac{4y}{y}}-3.1=5\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)
Tính diện tích miền hình phẳng giới hạn bới các đường y = x 2 - 2 x , y = 0 , x = - 10 , x = 10
A. S = 2000 3
B. S = 2008
C. S = 2008 3
D. S = 2000
Chọn đáp án C
Phương trình hoành độ giao điểm của đồ thị y = x 2 - 2 x và y = 0 là
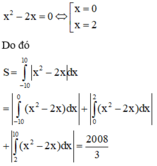
STUDY TIP |
Khi sử dụng MTCT tính tích phân mà không chia khoảng thì có sự sai khác về kết quả giữa các loại máy tính |
cho x + y =1 , x>0;y>0 tìm gtnn của
a) 1/x +1/y
b) a2/x+b2/y(a,b là hằng số dương đã cho)
c) (x+1/x)^2+(y+1/y)^2
Phần này chug: áp dụng Cauchy có: \(a+b\ge2\sqrt{ab}\Leftrightarrow ab\le\left(\frac{a+b}{2}\right)^2=\frac{1}{4}\)
a) \(A=\frac{1}{x}+\frac{1}{y}=\frac{x+y}{xy}=\frac{1}{xy}\ge\frac{1}{\frac{1}{4}}=4\)
b) Áp dụng BĐT Schwart có: \(\frac{a^2}{x}+\frac{b^2}{y}\ge\frac{\left(a+b\right)^2}{x+y}=\left(a+b\right)^2\)
c) đề câu này là \(x+\frac{1}{x}\)hay \(\frac{x+1}{x}\)vậy em?
1.Cho x^2+ 4x+1 = 0
Tính A= ( x + 1/x )^2 + (x^2 + 1/x^2 )^2 + ( x^3+ 1/x^3 )^2
2.Cho các số thực x, y khác 0 sao cho x+ 1/y và y+ 1/x là những số nguyên . CMR x^3y^3 + 1/x^3y^3 là số nguyên.
3.Cho x,y,z khác 0 tm x(y+z)^2+y(z+x)^2+z(x+y)^2=4xyz
Cho x,y,z khác 0 và x-y-z=0. Tính A= (1-z/x).(1-x/y).(1+y/z)
x-y-z=0
=> x=y+z
y=x-z
-z=y-x
B=(1-z/x)(1-x/y)(1+y/z)
B=((x-z)/x)((y-x)/y)((z+y)/z)
B=(y/x)(-z/y)(x/z)
B=(-zyx)/(xyz)
B=-1