Cho hàm số f(x) = (2m+1)x - 3m +2
a) Tìm m để phương trình f(x) = 0 có nghiệm x∈\([0;1]\)
b) Tìm m để f(x)≥0 có nghiệm x ∈\([\)\(-1;2]\)
Cho hàm số F(x) = (m + 1)x2 - 2mx + m - 2 (m là tham số). a) Tìm m để phương trình f(x) = 0 có hai nghiệm trái dấu? b) Tìm m để bất phương trình f(x) < 0 có một nghiệm đúng với mọi x.
Với thì PT có nghiệm (chọn)
Với thì là đa thức bậc 2 ẩn
có nghiệm khi mà
Tóm lại để có nghiệm thì
Cho f(x)=x^2 -2(m-2)x+m+10. Định m để:
a. Phương trình f(x)=0 có một nghiệm x= 1 và tính nghiệm kia
b. Phương trình f(x)=0 có nghiệm kép. Tính nghiệm kép đó.
c. Tìm m để phương trình f(x)=0 có 2 nghiệm âm phân biệt.
d. Tìm m để f(x)<0 có nghiệm đúng với mọi xϵR
a.
\(f\left(x\right)=0\) có nghiệm \(x=1\Rightarrow f\left(1\right)=0\)
\(\Rightarrow1-2\left(m-2\right)+m+10=0\)
\(\Rightarrow m=15\)
Khi đó nghiệm còn lại là: \(x_2=\dfrac{m+10}{x_1}=\dfrac{25}{1}=25\)
b.
Pt có nghiệm kép khi: \(\Delta'=\left(m-2\right)^2-\left(m+10\right)=0\)
\(\Rightarrow m^2-5m-6=0\Rightarrow\left[{}\begin{matrix}m=-1\\m=6\end{matrix}\right.\)
Với \(m=-1\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=-3\)
Với \(m=6\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=4\)
c.
Pt có 2 nghiệm âm pb khi:
\(\left\{{}\begin{matrix}\Delta'=m^2-5m-6>0\\x_1+x_2=2\left(m-2\right)< 0\\x_1x_2=m+10>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< -1\\m>6\end{matrix}\right.\\m< 2\\m>-10\end{matrix}\right.\) \(\Rightarrow-10< m< -1\)
d.
\(f\left(x\right)< 0;\forall x\in R\Rightarrow\left\{{}\begin{matrix}a=1< 0\left(\text{vô lý}\right)\\\Delta'=m^2-5m-6< 0\end{matrix}\right.\)
Không tồn tại m thỏa mãn
Cho hàm số f(x) có đạo hàm liên tục trên R và thỏa mãn f(x)>0,∀x∈R. Biết f(0)=1 và (2-x)f(x)-f' (x)=0. Tìm tất cả các giá trị thực của tham số m để phương trình f(x)=m có hai nghiệm phân biệt.
A. m< e 2 .
B. 0<m< e 2 .
C. 0<m≤ e 2 .
D. m > e 2
Cho hàm số f(x) có đạo hàm liên tục trên và thỏa mãn f ( x ) > 0 , ∀ ∈ ℝ . Biết f(0) = 1 và f ' x f x = 2 - 2 x . Tìm các giá trị thực của tham số m để phương trình f(x) = m có hai nghiệm thực phân biệt.
A. m > e
B. 0 < m ≤ 1
C. 0 < m < e
D. 1 < m < e
Đáp án C
Với f x > 0 , ∀ x ∈ ℝ . Xét biểu thức f ' x f x = 2 - 2 x *
Lấy nguyên hàm 2 vế (*), ta được ∫ d f x f x = ∫ 2 - 2 x d x
⇔ ∫ d f x f x = - x 2 + 2 x + C ⇔ ln f x = - x 2 + 2 x + C
Mà f(0) =1 suy ra C = lnf(0) = ln1 = 0. Do đó f x = e - x 2 + 2 x
Xét hàm số f x = e - x 2 + 2 x trên - ∞ ; + ∞ , có f ' x = - 2 x + 2 = 0 ⇔ x = 1
Tính giá trị f 1 = e ; lim x → - ∞ f x = 0 ; lim x → - ∞ f x = 0
Suy ra để phương trình f(x) = m có hai nghiệm thực phân biệt ⇔ 0 < m < e .
Cho hàm số g ( x ) = x 2 + 1 và hàm số f ( x ) = x 3 - 3 x 2 + 1 . Tìm m để phương trình f ( g ( x ) ) - m = 0 có 4 nghiệm phân biệt.
A. - 3 < m < 1
B. - 3 < m ≤ 1
C. - 3 ≤ m ≤ - 1
D. m > - 1
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình bên. Có bao nhiêu số thực m để bất phương trình m x + m 2 10 - x + 3 m + 1 . f ( x ) ≥ 0 nghiệm đúng với mọi x ∈ - 2 ; 3
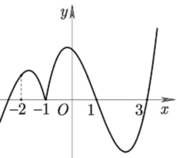
A. 1
B. 3
C. 0
D. 2
Đặt ![]() Ta có
Ta có ![]()
Trên đoạn [-2;3] ta có f(x) chỉ đổi dấu khi qua điểm x=1 Do vậy trước tiên cần có x=1 là nghiệm của ![]()
![]()
Điều kiện đủ:
+) Với m=−1
![]()
(đúng)
+) Với m = - 1 3

(đúng).
Vậy m = 1 , m = - 1 3 là các giá trị cần tìm.
Chọn đáp án D.
Cho hàm số f(x) có đạo hàm liên tục trên ℝ và thỏa mãn f(x) > 0, ∀ x ∈ ℝ . Biết f(0) = 1 và f ' ( x ) = ( 6 x - 3 x 2 ) f ( x ) . Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = m có nghiệm duy nhất.
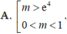
![]()
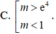
![]()
cho hàm số f(x)=sin2x+2(1-2m)cos2x-2mx+1. Với giá trị nào của tham số m thì phương trình f'(x)=0 có nghiệm
\(f'\left(x\right)=2cos2x-4\left(1-2m\right)sin2x-2m\)
Phương trình \(f'\left(x\right)=0\) có nghiệm
\(\Leftrightarrow2cos2x-4\left(1-2m\right)sin2x=2m\) có nghiệm
\(\Leftrightarrow cos2x-2\left(1-2m\right)sin2x=m\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(1^2+4\left(1-2m\right)^2\ge m^2\)
\(\Leftrightarrow15m^2-16m+5\ge0\)
\(\Leftrightarrow15\left(m-\dfrac{8}{15}\right)^2+\dfrac{11}{15}\ge0\) (luôn đúng)
Vậy \(f'\left(x\right)=0\) có nghiệm với mọi m
Cho hàm số y = f (x) có đạo hàm liên tục trên ℝ , với f (x) > 0 và f (0) = 1. Biết rằng f ' ( x ) + 3 x x - 2 f ( x ) = 0 , ∀ x ∈ ℝ . Tìm tất cả các giá trị thực của tham số m để phương trình f x + m = 0 có bốn nghiệm thực phân biệt.
A. 1 < m < e 4
B. - e 6 < m < - 1
C. - e 4 < m < - 1
D. 0 < m < e 4
Đáp án C

Bảng biến thiên của hàm số f(x) là
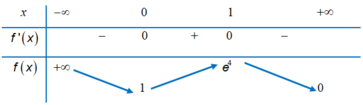
Hàm số f x là hàm số chẵn trên ℝ nên đồ thị của hàm số nhận trục tung làm trục đối xứng. Do đó phương trình f ( x ) + m = 0 có bốn nghiệm thực phân biệt khi và chỉ khi phương trình f ( x ) + m = 0 có hai nghiệm dương phân biệt hay phương trình f ( x ) = - m có hai nghiệm dương phân biệt
⇔ 1 < - m < e 4 ⇔ - e 4 < m < - 1
1.tìm m để phương trình \(x^2+\dfrac{1}{x^2}-2m\left(x+\dfrac{1}{x}\right)+1+2m=0\left(x\ne0\right)\) có nghiệm
2. cho hàm số y=f(x)=\(x^2-4x+3\)
tìmcác giá trị nguyên của m để
\(f^2\left(\left|x\right|\right)+\left(m-2\right)f\left(\left|x\right|\right)+m-3=0\) có 6 nghiệm phân biệt
\(1.x^2+\dfrac{1}{x^2}-2m\left(x+\dfrac{1}{x}\right)+1+2m=0\left(1\right)\)\(đặt:x^2+\dfrac{1}{x^2}=t\)
\(x>0\Rightarrow t\ge2\sqrt{x^2.\dfrac{1}{x^2}}=2\)
\(x< 0\Rightarrow-t=-x^2+\dfrac{1}{\left(-x^2\right)}\ge2\Rightarrow t\le-2\)
\(\Rightarrow t\in(-\infty;-2]\cup[2;+\infty)\left(2\right)\)
\(\Rightarrow\left(1\right)\Leftrightarrow t^2-2mt+2m-1=0\)
\(\Leftrightarrow\left(t-1\right)\left(t-2m+1\right)=0\Leftrightarrow\left[{}\begin{matrix}t=1\notin\left(2\right)\\t=2m-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2m-1\le-2\\2m-1\ge2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}m\le-\dfrac{1}{2}\\m\ge\dfrac{3}{4}\end{matrix}\right.\)
\(2.\) \(f^2\left(\left|x\right|\right)+\left(m-2\right)f\left(\left|x\right|\right)+m-3=0\left(1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}f\left(\left|x\right|\right)=-1\\f\left(\left|x\right|\right)=3-m\end{matrix}\right.\)
\(dựa\) \(vào\) \(đồ\) \(thị\) \(f\left(\left|x\right|\right)\) \(\Rightarrow f\left(\left|x\right|\right)=-1\) \(có\) \(2nghiem\) \(pb\)
\(\left(1\right)có\) \(6\) \(ngo\) \(pb\Leftrightarrow\left\{{}\begin{matrix}-1< 3-m< 3\\3-m\ne-1\\\end{matrix}\right.\)\(\Leftrightarrow0< m< 4\)
\(\Rightarrow m=\left\{1;2;3\right\}\)