Cho hình vuông ABCD, M tùy ý (M∈BD). Kẻ ME⊥AB; MF⊥AD.
a)cm: DE=CF và DE⊥CF
b)Cm: 3 đoạn thẳng DE, BF, CM đồng quy.
c) Xác định vị trí M trên BD để diện tích tứ giác AEMF lớn nhất.
Những câu hỏi liên quan
. Cho hình vuông ABCD, M là một điểm tùy ý trên đường chéo BD. Kẻ ME vuông AB, MF vuông AD .
a) Chứng minh DE=CF .
b) Chứng minh ba đường thẳng DE, BF, CM đồng quy.
Xét \(\Delta DFM\) vuông tại F có \(\angle FDM=45\Rightarrow\Delta DFM\) vuông cân tại F
\(\Rightarrow DF=FM\)
Vì \(\angle MFA=\angle MEA=\angle EAF=90\Rightarrow AEMF\) là hình chữ nhật
\(\Rightarrow AE=FM=DF\)
Xét \(\Delta DCF\) và \(\Delta ADE:\) Ta có: \(\left\{{}\begin{matrix}AD=CD\\DF=AE\\\angle DAE=\angle CDF=90\end{matrix}\right.\)
\(\Rightarrow\Delta DCF=\Delta ADE\left(c-g-c\right)\Rightarrow DE=CF\)
b) \(\Delta DCF=\Delta ADE\Rightarrow\angle DCF=\angle ADE\)
\(\Rightarrow\angle DCF+\angle DFC=\angle ADE+\angle DFC\Rightarrow\angle ADE+\angle DFC=90\)
\(\Rightarrow DE\bot FC\)
Tương tự chứng minh được: \(BF\bot CE\)
Gọi giao điểm của DE,BF là H \(\Rightarrow H\) là trực tâm tam giác CEF
\(\Rightarrow CH\bot EF\left(1\right)\)
FM cắt CB tại G,CM cắt AD tại I
Dễ dàng chứng minh được DCFG là hình chữ nhật
\(\Rightarrow CG=DF=AE\)
Ta có: \(MG=FG-FM=CD-FD==AD-FD=AF\)
Xét \(\Delta CMG\) và \(\Delta EFA:\) Ta có: \(\left\{{}\begin{matrix}MG=AF\\AE=CG\\\angle CGM=\angle EAF=90\end{matrix}\right.\)
\(\Rightarrow\Delta CMG=\Delta EFA\left(c-g-c\right)\Rightarrow\angle AFE=\angle CMG=\angle FMI\)
\(\Rightarrow\angle AFE+\angle FIM=\angle FMI+\angle FIM\Rightarrow\angle AFE+\angle FIM=90\)
\(\Rightarrow CM\bot EF\left(2\right)\)
Từ (1) và (2) \(\Rightarrow C,H,M\) thẳng hàng \(\Rightarrow\) đpcm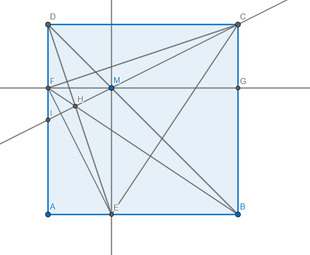
Đúng 1
Bình luận (0)
15 tháng 10 2023 lúc 14:32
Cho hình vuông ABCD cạnh a. M là 1 điểm tùy ý trên đường chéo BD. Kẻ ME vuông góc với AB, MF vuông góc với AD ( E thuộc AB, F thuộc AD).
1.Chứng minh rằng: DE = CF
2.Chứng minh rằng DE, BF, CM đồng quy.
3.Xác định vị trí của M trên cạnh BD để diện tích của AEMF lớn nhất
Xem chi tiết
Cho hình vuông ABCD. M là một điểm tùy ý trên đường chéo BD. KẺ ME vuông góc AB, MF vuông góc AD
a) Chứng minh DE=CF Và DE vuông góc CF
b) CM=EF,CM vuông góc với EF
c) CM,BF,DE đồng quy
Cho hình vuông ABCD, M là một điểm tùy ý trên đường chéo BD. Kẻ ME ^ AB; MF ^ AD.
a) Chứng minh: DE = CF;
b) Chứng minh DE ^ FC;
c) Xác định vị trí của điểm M để diện tích tứ giác AMEF lớn nhất
a) Chứng minh AE = PM = DF ÞDAED = DDFC Þ ĐPCM;
b) Từ câu a chứng minh được DE ^ FC.
c) Gọi cạnh hình vuông a. Chu vi hình chữ nhật AEMF = 2a;
Þ ME + MF = a không đổi;
⇒ S A E M F = M E . M F ≤ M E + M F 2 2 = a 2 4
Vậy lớn nhất khi ME = MF hay M là trung điểm BD
Đúng 0
Bình luận (0)
Cho hình vuông ABCD. M là một điểm tùy ý trên đường chéo BD. KẺ ME vuông góc AB, MF vuông góc AD
a) Chứng minh DE=CF Và DE vuông góc CF
B) CMR ba đường thẳng DE, BF, CM đồng quy
Câu hỏi của Kunzy Nguyễn - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo bài tương tự tại đây nhé.
Đúng 2
Bình luận (0)
8. cho hcn ABCD đươngf chéo AC và BD cắt nhau tai O . Lấy P là 1 điểm tùy ý trên OB .Gọi M là điểm đx vs C qua P . từ M kẻ ME vuông góc vs đường thẳng AD ( E ∈ AD), kẻ MF vuông goác vs đường thẳng AB (F ∈ AB )
a) cmr AEMF là hcn
b) cmr AMBD là hình thang
c) cm E,F,P thẳng hàng
d) xác định vị trí của P để AMBD là hình thang cân
Chưa ra câu c ^^
a/ Xét tứ giác AEMF có
\(\widehat{EAF}=\widehat{AEM}=\widehat{AFM}=90^o\)
=> Tứ giác AEMF là hcn
b/ Xét t/g AMC có OP là đường trung bình
=> OP // AM
=> BD // AM
=> Tứ giác AMBD là hình thang
d/ Để hình thang AMBD là htc thì AD = BM
=> BM = BC
=> t/g BMC cân tại B có BP là đương trung tuyến
=> CP ⊥ BP tại P
Đúng 1
Bình luận (0)
Cho hình vuông ABCD. Lấy điểm M tùy ý trên BD. Từ M kẻ ME vuông góc với AB, MF vuông góc với AD. chứng minh:
a) CF = DE, CF vuông góc với DE
b) CM = FE, CM vuông góc với FE
c) CM, BF, DE đồng qui
Cho hình vuông ABCD, điểm M tùy ý trên đường chéo BD. kẻ ME vuông góc với AB tại E, MF vuông góc với AD tại F.
a, Tứ giác AEMF là hình gì? Vì sao?
b, CM: AF = BE và DE vuông góc với CF.
c, Ba đường DF, BF, CM đồng quy.
Câu hỏi của Kunzy Nguyễn - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo bài tương tự tại đây nhé.
Đúng 0
Bình luận (0)
cho hình vuông ABCD, M là 1 điểm tùy ý trên đường chéo BD. Kẻ \(ME\perp AB⋮E,MF\perp AD⋮F\)
Xác định vị trí của điểm M để diện tích tứ giác AEMF lớn nhất
Cho hình vuông ABCD
M là 1 điểm tùy ý thuộc BD
Kẻ ME vuông góc với AB; MF vuông góc với AD
ME cắt CD ở K
a. CM: DE, BF, CM đồng quy
b. H là giao điểm của CM, EF
CM: tam giác BHK vuông ở H