Nhập số tự nhiên n và số thực x. Tính
A=sinx+sin2x+...+sinnx
B=sinx+sinx2+...+sinxn
Những câu hỏi liên quan
Cho các số thực x,y thay đổi thỏa mãn
log
2
sin
x
+
2
cos
x
+
2
2
cos
x
-
sin
x...
Đọc tiếp
Cho các số thực x,y thay đổi thỏa mãn log 2 sin x + 2 cos x + 2 = 2 cos x - sin x + 3 . Gọi - a b với a , b ∈ ℕ * , a b tối giản là giá trị nhỏ nhất của biểu thức P = 3 cos 3 x + sin 2 x - 5 cos x Tính T = a +b
A. T = 200
B. T = 257
C. T = 210
D. T = 240
Cho các số thực x,y thay đổi thỏa mãn
log
2
sinx
+
2
cosx
+
2
2
cosx
-
sinx
+
3
. Gọi -
a
b
...
Đọc tiếp
Cho các số thực x,y thay đổi thỏa mãn log 2 sinx + 2 cosx + 2 = 2 cosx - sinx + 3 . Gọi - a b với a ∈ N * , b ∈ N * , a b tối giản là giá trị nhỏ nhất của biểu thức P= 3 cos 3 x + sin 2 x - 5 cosx . Tính T=a+b.
A.T=200.
B. T=257.
C. T=210.
D. T=240
Tìm GTLN và GTNN của hàm số : 1. y = sinx + 2cosx +1 / 2sinx + cosx + 3
2.y= 2sin^2sinx - 3 sinx cosx + cos^2 x
Giải phương trình : 1. 2sin^2 * 2x + sin7x -1 = sinx
2.cos 4x + 12 sin^2 x -1 = 0
Cho x thỏa mãn phương trình
sin
2
x
+
sin
x
−
cos
x
1
. Tính
sin
x
−
π
4
.
A.
sin
x
−
π
4
0
h
o
ặ...
Đọc tiếp
Cho x thỏa mãn phương trình sin 2 x + sin x − cos x = 1 . Tính sin x − π 4 .
A. sin x − π 4 = 0 h o ặ c sin x − π 4 = 1
B. sin x − π 4 = 0 h o ặ c sin x − π 4 = 2 2
C. sin x − π 4 = − 2 2
D. sin x − π 4 = 0 h o ặ c sin x − π 4 = − 2 2
Đặt t = sin x − cos x = 2 sin x − π 4 .
Điều kiện − 2 ≤ t ≤ 2 .
Ta có t 2 = sin x − cos x 2 = sin 2 x + cos 2 x − 2 sin x cos x ⇒ sin 2 x = 1 − t 2 .
Phương trình đã cho trở thành 1 − t 2 + t = 1 ⇔ t 2 − t = 0 ⇔ t = 0 t = 1 .
Với t = 1, ta được 2 sin x − π 4 = 1 ⇔ sin x − π 4 = 1 2 .
Với t = 0, ta được 2 sin x − π 4 = 0 ⇔ sin x − π 4 = 0.
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho x thỏa mãn phương trình sin2x+sinx-cosx1 Tính
sin
x
-
π
4
?
Đọc tiếp
Cho x thỏa mãn phương trình
sin2x+sinx-cosx=1 Tính sin x - π 4 ?
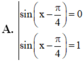
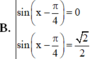
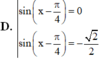
Chọn B
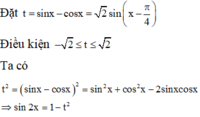
Bổ trợ kiến thức: Ta có thế giải bằng máy tính cầm tay CASIO fx-570VN PLUS như sau, đâu tiên dùng lệnh SHIFT SOLVE để xem 1 nghiệm bất kì có thể có của phương trình đã cho:
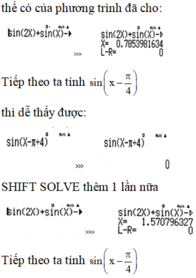
Đến đây ta dễ dàng chọn được phương án B là phương án đúng thay cho lời giải tự luận nhiều phức tạp.
Đúng 0
Bình luận (0)
Chứng minh các đẳng thức :
a) sin3x = 3sinx - 4sin3x
b) tan 2x + 1/cos2x = 1-2sin2x/1-sin2x
c) (cosx+sinx/cosx-sinx) - (cosx-sinx/cosx+sinx) = 2tan 2x
d) sin2x/1+cos2x = tanx
e)
a/ \(sin3x=sin\left(2x+x\right)=sin2xcosx+cos2x.sinx\)
\(=2sinxcos^2x+\left(1-2sin^2x\right)sinx=2sinx\left(1-sin^2x\right)+sinx-2sin^3x\)
\(=3sinx-4sin^3x\)
b/
\(tan2x+\frac{1}{cos2x}=\frac{sin2x}{cos2x}+\frac{1}{cos2x}=\frac{sin2x+1}{cos2x}=\frac{2sinxcosx+sin^2x+cos^2x}{cos^2x-sin^2x}\)
\(=\frac{\left(sinx+cosx\right)^2}{\left(sinx+cosx\right)\left(cosx-sinx\right)}=\frac{sinx+cosx}{cosx-sinx}=\frac{\left(sinx+cosx\right)\left(cosx-sinx\right)}{\left(cos-sinx\right)^2}\)
\(=\frac{cos^2x-sin^2x}{cos^2x+sin^2x-2sinxcosx}=\frac{1-2sin^2x}{1-sin2x}\)
c/
\(\frac{cosx+sinx}{cosx-sinx}-\frac{cosx-sinx}{cosx+sinx}=\frac{\left(cosx+sinx\right)^2-\left(cosx-sinx\right)^2}{cos^2x-sin^2x}\)
\(=\frac{2sinxcosx+2sinxcosx}{cos2x}=\frac{4sinxcosx}{cos2x}=\frac{2sin2x}{cos2x}=2tan2x\)
d/
\(\frac{sin2x}{1+cos2x}=\frac{2sinxcosx}{1+2cos^2x-1}=\frac{2sinxcosx}{2cos^2x}=\frac{sinx}{cosx}=tanx\)
e/
Đúng 0
Bình luận (0)
Tìm cực trị của các hàm số sau:
a) y = sin2x
b) y = cosx − sinx
c) y = sin 2 x
a) y = sin2x
Hàm số có chu kỳ T = π
Xét hàm số y=sin2x trên đoạn [0;π], ta có:
y' = 2cos2x
y' = 0 ⇔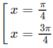 
Bảng biến thiên:
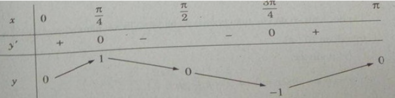
Do đó trên đoạn [0;π] , hàm số đạt cực đại tại π/4 , đạt cực tiểu tại 3π/4 và y C D = y(π/4) = 1; y C T = y(3π/4) = −1
Vậy trên R ta có:
y C Đ = y(π/4 + kπ) = 1;
y C T = y(3π/4 + kπ) = −1, k∈Z
b) Hàm số tuần hoàn chu kỳ nên ta xét trên đoạn [−π;π].
y′ = − sinx – cosx
y′ = 0 ⇔ tanx = −1 ⇔ x = −π4 + kπ, k∈Z
Lập bảng biến thiên trên đoạn [−π;π]
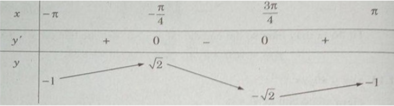
Hàm số đạt cực đại tại x = −π4 + k2π , đạt cực tiểu tại x = 3π4 + k2π (k∈Z) và
y C Đ = y(−π4 + k2π) = 2 ;
y C T = y(3π4 + k2π) = − 2 (k∈Z).
c) Ta có:
Do đó, hàm số đã cho tuần hoàn với chu kỳ π.
Ta xét hàm số y trên đoạn [0;π]:
y′ = sin2x
y′ = 0 ⇔ sin2x = 0 ⇔ x = kπ/2 (k∈Z)
Lập bảng biến thiên trên đoạn [0,π]
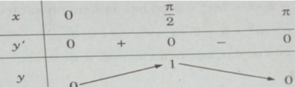
Từ đó, ta thấy hàm số đạt cực tiểu tại x = kπ/2 với k chẵn, đạt cực đại tại x = kπ/2 với k lẻ, và
y C T = y(2mπ) = 0; yCT = y(2mπ) = 0;
y C Đ = y((2m+1)π/2) = 1 (m∈Z)
Đúng 0
Bình luận (0)
Có bao nhiêu số nguyên m để phương trình
sin
2
x
-
sin
x
m+
2
m
+
3
sin
x
có nghiệm thực. A. 7 B. 2. C. 3. D. 6.
Đọc tiếp
Có bao nhiêu số nguyên m để phương trình sin 2 x - sin x = m+ 2 m + 3 sin x có nghiệm thực.
A. 7
B. 2.
C. 3.
D. 6.
Có bao nhiêu số nguyên m để phương trình
s
i
n
2
x
-
s
i
n
x
m
+
2
m
+
3
sin
x
có nghiệm thực. A. 7. B. 2. C. 3. D. 6.
Đọc tiếp
Có bao nhiêu số nguyên m để phương trình s i n 2 x - s i n x = m + 2 m + 3 sin x có nghiệm thực.
A. 7.
B. 2.
C. 3.
D. 6.
