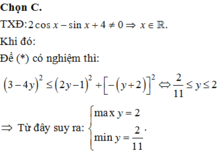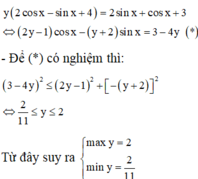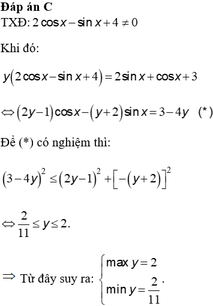GtNN của hs y=sinx-cox/2sinx+cosx+3

Những câu hỏi liên quan
Tìm GTLN và GTNN của hàm số : 1. y = sinx + 2cosx +1 / 2sinx + cosx + 3
2.y= 2sin^2sinx - 3 sinx cosx + cos^2 x
Giải phương trình : 1. 2sin^2 * 2x + sin7x -1 = sinx
2.cos 4x + 12 sin^2 x -1 = 0
Tìm GTLN và GTNN của hàm số:
y
2
sin
x
+
cos
x
+
3
2
cos
x
-
sin
x
+
4
Đọc tiếp
Tìm GTLN và GTNN của hàm số: y = 2 sin x + cos x + 3 2 cos x - sin x + 4
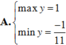
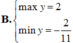
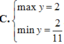
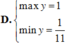
Tìm GTLN và GTNN của hàm số
y
2
sin
x
+
cos
x
+
3
2
cos
x
-
sin
x
+
4
là
Đọc tiếp
Tìm GTLN và GTNN của hàm số y = 2 sin x + cos x + 3 2 cos x - sin x + 4 là
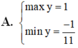
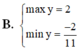
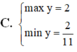
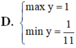
Tìm GTLN và GTNN của hàm số
y
2
sin
x
+
cos
x
+
3
2
cos
x
-
sin
x
+
4
là: A.
m
a...
Đọc tiếp
Tìm GTLN và GTNN của hàm số y = 2 sin x + cos x + 3 2 cos x - sin x + 4 là:
A. m a x y = 1 m i n y = - 1 11
B. m a x y = 2 m i n y = - 2 11
C. m a x y = 2 m i n y = 2 11
D. m a x y = 1 m i n y = 1 11
Tìm GTNN của hàm số \(y=\dfrac{sinx+1}{cosx+2}\)
Tìm GTLN của hàm số \(y=\dfrac{cosx+2sinx+3}{2cosx-sinx+4}\)
1. Do \(\cos x+2>0\forall x\in R\) \(\Rightarrow\) Hàm số xác định \(\forall x\in R\)
\(y=\dfrac{\sin x+1}{\cos x+2}\)
\(\Leftrightarrow\)\(y\cos x-\sin x=1-2y\)
pt có nghiệm \(\Leftrightarrow y^2+\left(-1\right)^2\ge\left(1-2y\right)^2\)
\(\Leftrightarrow3y^2-4y\le0\)
\(\Leftrightarrow0\le y\le\dfrac{4}{3}\)
2. \(y=\dfrac{\cos x+2\sin x+3}{2\cos x-\sin x+4}\)
\(\Leftrightarrow\left(2y-1\right)\cos x-\left(y+2\right)\sin x=3-4y\)
pt có nghiệm \(\Leftrightarrow\left(2y-1\right)^2+\left(y+2\right)^2\ge\left(3-4y\right)^2\)
\(\Leftrightarrow11y^2-24y+4\le0\)
\(\Leftrightarrow\dfrac{2}{11}\le y\le2\)
kiểm tra giúp mình xem có sai sót gì không...
Đúng 0
Bình luận (2)
giá trị nhỏ nhất và giá trị lớn nhất của hám số y= sinx+cos/2sinx-cox +3 lần lượt là:
\(y=\dfrac{sinx+cosx}{2sinx-cosx+3}\Rightarrow2y.sinx-y.cosx+3y=sinx+cosx\)
\(\Leftrightarrow\left(1-2y\right)sinx+\left(y+1\right)cosx=3y\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\left(1-2y\right)^2+\left(y+1\right)^2\ge9y^2\)
\(\Rightarrow2y^2+y-1\le0\)
\(\Rightarrow-1\le y\le\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
tìm GTLN,GTNN của hàm số
a/ y= sin2x + (\(\sqrt{3}\) +1) cos2x +sin4 x -cos4x -1
b/ (sinx -2cosx)(2sinx+cosx)-1
c/ y= (Sinx-cosx)2+2cos2x+3sinxcosx
giúp em giải chi tiết với ạ
a/ \(y=sin2x+\left(\sqrt{3}+1\right)cos2x+sin^2x-cos^2x-1\)
\(=sin2x+\sqrt{3}cos2x-1=2sin\left(2x+\frac{\pi}{3}\right)-1\)
Do \(-1\le sin\left(2x+\frac{\pi}{3}\right)\le1\Rightarrow-3\le y\le1\)
b/ \(y=2sin^2x-2cos^2x-3sinx.cosx-1\)
\(=-2cos2x-\frac{3}{2}sin2x-1=-\frac{5}{2}\left(\frac{3}{5}sinx+\frac{4}{5}cosx\right)-1\)
\(=-\frac{5}{2}sin\left(x+a\right)-1\Rightarrow-\frac{7}{2}\le y\le\frac{3}{2}\)
c/ \(y=1-sin2x+2cos2x+\frac{3}{2}sin2x=\frac{1}{2}sin2x+2cos2x+1\)
\(=\frac{\sqrt{17}}{2}\left(\frac{1}{\sqrt{17}}sin2x+\frac{4}{\sqrt{17}}cos2x\right)+1=\frac{\sqrt{17}}{2}sin\left(2x+a\right)+1\)
\(\Rightarrow-\frac{\sqrt{17}}{2}+1\le y\le\frac{\sqrt{17}}{2}+1\)
Đúng 0
Bình luận (0)
1. Với những giá trị nào của x ta có đẳng thức sau
A = 1/ 1+ tan^2x = cos^2x
2. Tìm TXD của hàm số
y = 1 +tanx / ✓1 - sinx
y = ✓1-2cosx / √3 - tanx ( dưới mẫu căn nơi số 3 , còn tử căn hết biểu thức)
3. GTNN của hs
y = 1 - cosx - sinx
4. GTLN của HS
y = 2 + |cosx| + |sinx|
8. GTLN và GTNN của hs y = cosx^2 + 2cos2x là?
10. GTLN của HS y = 1 -2cosx - cos^2x là?
14. HS y = |sinx| là hs tuần hoàn với chu kỳ?
8.
\(y=cos^2x+2\left(2cos^2x-1\right)=5cos^2x-2\)
Do \(0\le cos^2x\le1\Rightarrow-2\le y\le3\)
\(y_{min}=-2;y_{max}=3\)
10.
\(y=2-\left(cosx+1\right)^2\le2\)
\(y_{max}=2\)
14.
Hàm tuần hoàn với chu kì \(T=\pi\)
Đúng 0
Bình luận (0)