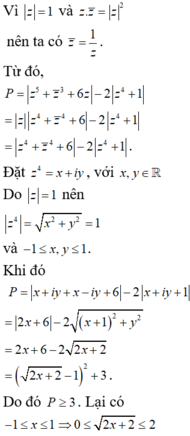Tính giá trị của P = 2y4 + 7x - 2z4 biết x,y,z nguyên và thỏa mãn ( x2 + 1 )2 + ( y - z )2 = 100
Những câu hỏi liên quan
27 tháng 5 2022 lúc 11:13
cho ba số thực dương x,y,z thỏa mãn điều kiện x2≥y+z .Tìm giá trị nhỏ nhất của biểu thức : P = \(\dfrac{1}{x^2}\left(y^2+z^2\right)+\dfrac{7x^2}{2}\left(\dfrac{1}{y^2}+\dfrac{1}{z^2}\right)+2007\)
Lời giải:
Sửa: $x^2\geq y^2+z^2$
Áp dụng BĐT Cauchy-Schwarz:
$P\geq \frac{y^2+z^2}{x^2}+\frac{7x^2}{2}.\frac{4}{y^2+z^2}+2007$
$=\frac{y^2+z^2}{x^2}+\frac{14x^2}{y^2+z^2}+2007$
$=\frac{y^2+z^2}{x^2}+\frac{x^2}{y^2+z^2}+\frac{13x^2}{y^2+z^2}+2007$
$\geq 2+\frac{13x^2}{y^2+z^2}+2007$ (áp dụng BĐT Cô-si)
$\geq 2+13+2007=2022$ (do $x^2\geq y^2+z^2$)
Vậy $P_{\min}=2022$
Đúng 1
Bình luận (0)
Giá trị của y thỏa mãn x2+y2+z2=xy+3y+2z-4 biết x, y, z là số nguyên.
Cho 3 số x , y , z , thỏa mãn :
\(\frac{19}{x+y}+\frac{19}{y+z}+\frac{19}{z+x}=\frac{7x}{y+z}+\frac{7x}{z+x}+\frac{7x}{x+y}=\frac{133}{10}\)
Tính giá trị biểu thức : \(M=\left(x+y+z\right)^2\)
Biết rằng x,y và z là các số thực và thỏa mãn:\(\frac{x-1}{2}\)=\(\frac{y}{3}\)=\(\frac{z+2}{6}\). Biết rằng x+y+z=-5.Tính các giá trị của x,y và z
Cho x,y,z thỏa mãn đk x/(y+z)+y/(x+z)+z/(x+y)=1
Tính giá trị của S=x^2/(y+z)+y^2/(x+z)+z^2/(x+y)
\(\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}=1\Leftrightarrow\left(x+y+z\right)\left(\frac{x}{y+z}+\frac{y}{x+z}+\frac{z}{x+y}\right)=x+y+z\)
<=>\(\frac{x^2+x\left(y+z\right)}{y+z}+\frac{y^2+y\left(z+x\right)}{z+x}+\frac{z^2+z\left(x+y\right)}{x+y}=x+y+z\)
<=>\(\frac{x^2}{y+z}+x+\frac{y^2}{z+x}+y+\frac{z^2}{x+y}+z=x+y+z\)
<=>\(S=\frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}=0\)
Đúng 1
Bình luận (1)
x/(y+z)+y/(x+z)+z/(x+y)=1
=>\(\frac{x^2}{\left(y+z\right)^2}\)+\(\frac{y^2}{\left(x+z\right)^2}\)+\(\frac{z^2}{\left(x+y\right)^2}\)+2(\(\frac{xy}{\left(y+z\right)\cdot\left(x+z\right)}\)+\(\frac{yz}{\left(x+z\right)\left(x+y\right)}\)+\(\frac{zx}{\left(z+y\right)\cdot\left(x+y\right)}\))=1
Đúng 0
Bình luận (0)
Cho zx+yi với
x
,
y
∈
ℝ
là số phức thỏa mãn điều kiện
z
→
+
2
-
3
i
≤
z
+
i
-
2
≤
5
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu...
Đọc tiếp
Cho z=x+yi với x , y ∈ ℝ là số phức thỏa mãn điều kiện z → + 2 - 3 i ≤ z + i - 2 ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 y . Tính M+m.
A. 60 + 2 10
B. 156 6 - 20 10 .
C. 60 - 2 10 .
D. 156 5 + 20 10
Cho
z
x
+
y
i
x
,
y
∈
R
là số phức thỏa mãn điều kiện
z
¯
+
2...
Đọc tiếp
Cho z = x + y i x , y ∈ R là số phức thỏa mãn điều kiện z ¯ + 2 - 3 i ≤ z + i - 2 ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 y . Tính M + m
A. 156 5 - 20 10
B. 60 - 20 10
C. 156 5 + 20 10
D. 60 + 20 10
Chọn đáp án B
Từ giả thiết ta có:
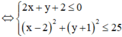
Suy ra tập hợp các điểm biểu diễn số phức z là miền mặt phẳng
(T) thỏa mãn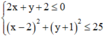 
(miền tô đậm trong hình vẽ bên
Gọi A, B là các giao điểm của đường thẳng 2 x + y + 2 = 0 và đường tròn (C’) : x - 2 2 + y + 1 2 = 25
Ta tìm được A(2; -6) và B(-2; 2)
Ta có :
Đường tròn (C) cắt miền (T) khi và chỉ khi
Đúng 0
Bình luận (0)
Cho ba số nguyên x,y,z thỏa mãn x^2+y^2+z^2=1. Tìm giá trị nhỏ nhất của biểu thức:
Xy/z +xz/y + yz/x
Cho số phức z thỏa mãn
z
1
. Gọi m, M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của biểu thức
P
z
5
+
z
¯
3
+
6
z
-
2...
Đọc tiếp
Cho số phức z thỏa mãn z = 1 . Gọi m, M lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của biểu thức P = z 5 + z ¯ 3 + 6 z - 2 z 4 + 1 . Tính M-m.
