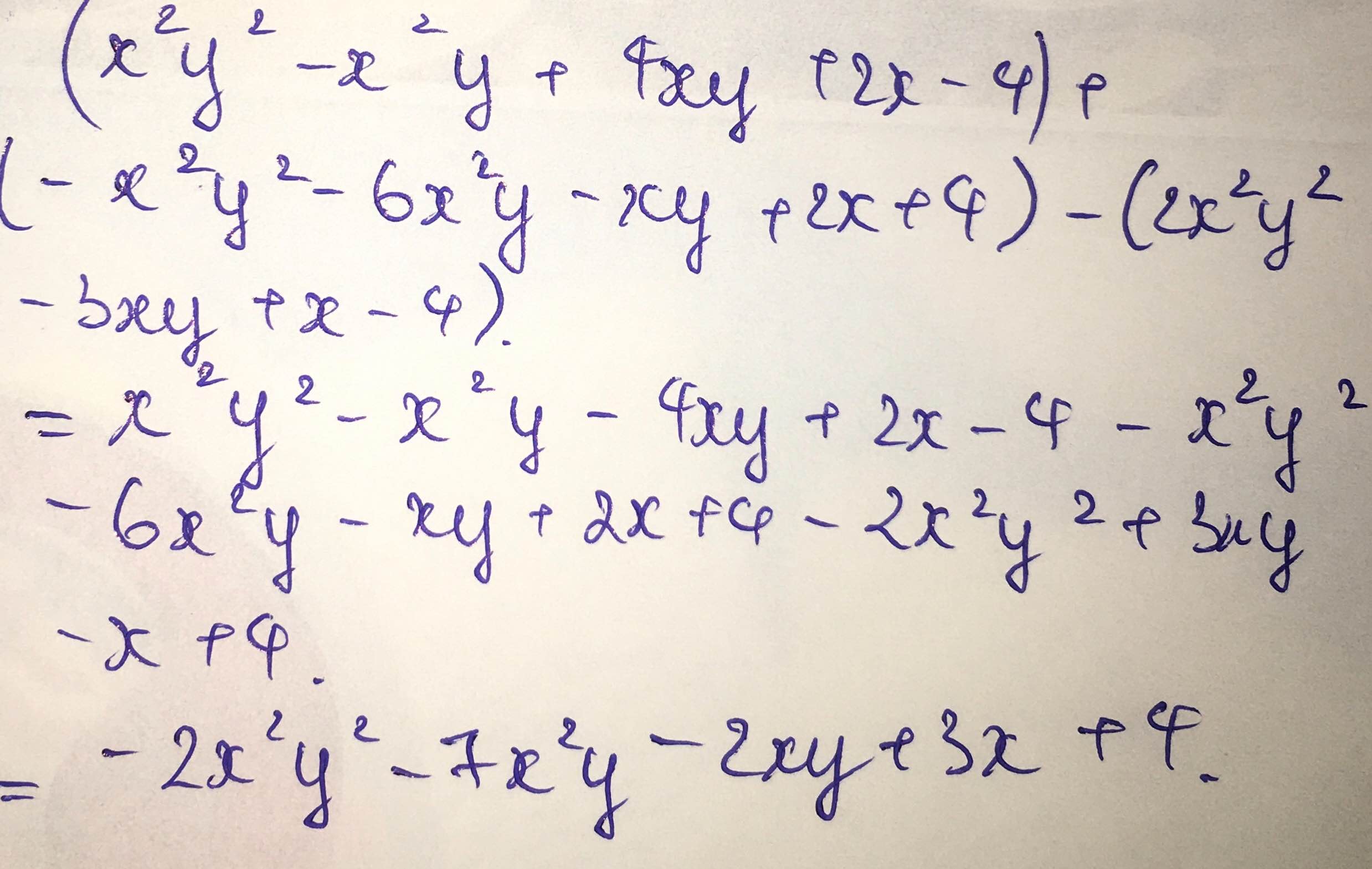4(2-x)^2+ xy -2y
Những câu hỏi liên quan
12 tháng 3 2022 lúc 21:56
(x^2y^2 - x^2y + 4xy + 2x - 4) + (-x^2y^2 - 6x^2y - xy + 2x+4) - (2x^2y^2 - 3xy +x - 4)
=
cho 2 số thực `x,y` thỏa mãn `x>0,y>2,x`\(\ne\)`2y`. CMR: \(\left(\dfrac{x-y}{2y-x}-\dfrac{x^2+y^2+y-2}{x^2-xy-2y^2}\right)\left(2x^2+y+2\right):\dfrac{x^4+4x^2y^2+y^4-4}{x^2+y+xy+x}=\dfrac{x+1}{2y-x}\)
Đề bài sai, đề đúng thì phân thức đằng sau dấu chia phải là:
\(\dfrac{4x^4+4x^2y+y^2-4}{x^2+y+xy+x}\)
Đúng 0
Bình luận (0)
chứng minh các đẳng thức sau:
a)(x+y)(x^3-x^2y+xy^2+y^3)=x^4+y^4
b)(x-y)(x^3+x^2y+xy^2+y^3)=x^4-y^4
c)(x+y)(x^4-x^3y+x^2y^2-xy^3+y^4)=x^5+y^5
d)(x-y)(x^4+x^3y+x^2y^2+xy^3+y^4)=x^5-y^5
đối với các câu này bạn hãy khai triển phần nào dài bằng hàng dẳng thức rồi thu gọn lại nếu đúng thì vế trái bằng vế phải
Đúng 0
Bình luận (0)
12 tháng 3 2022 lúc 21:20
(x^2y^2 - x^2y + 4xy + 2x - 4) + (-x^2y^2 - 6x^2y - xy + 2x+4)
=
chứng minh đẳng thức
\(\left(\frac{x-y}{2y-x}-\frac{x^2+y^2+y-2}{x^2-xy-2y^2}\right):\frac{x^4+4x^2y^2+y^4-4}{x^2+y+xy+x}:\frac{1}{2x^2+y+2}=\frac{x+1}{2y-x}\)
Rút gọn: \(\left(\frac{x-y}{2y-x}-\frac{x^2+y^2+y-2}{x^2-xy-2y^2}\right):\frac{4x^4+4x^2y+y^2-4}{x^2+xy+x+y}:\frac{x+1}{2y^2+y+2}\)
BT10: Thực hiện phép tính
\(a,\dfrac{4}{5}y^2x^5-x^3.x^2y^2\)
\(b,-xy^3-\dfrac{2}{7}y^2.xy\)
\(c,\dfrac{5}{6}xy^2z-\dfrac{1}{4}xyz.y\)
\(d,15x^4+7x^4-20x^2.x^2\)
\(e,\dfrac{1}{2}x^5y-\dfrac{3}{4}x^5y+xy.x^4\)
\(f,13x^2y^5-2x^2y^5+x^6\)
a: =-1/5x^5y^2
b: =-9/7xy^3
c: =7/12xy^2z
d: =2x^4
e: =3/4x^5y
f: =11x^2y^5+x^6
Đúng 1
Bình luận (0)
x,y dương thỏa mãn `xy+4<=2y`. Tìm max `P=(xy)/(x^2 +2y^2)`
\(2y\ge xy+4\ge2\sqrt{4xy}=4\sqrt{xy}\)
\(\Rightarrow y^2\ge4xy\Rightarrow\dfrac{y}{x}\ge4\)
\(P=\dfrac{xy}{x^2+2y^2}=\dfrac{1}{\dfrac{x}{y}+\dfrac{2y}{x}}=\dfrac{1}{\dfrac{1}{16}\left(\dfrac{16x}{y}+\dfrac{y}{x}\right)+\dfrac{31}{16}.\dfrac{y}{x}}\)
\(\Rightarrow P\le\dfrac{1}{\dfrac{1}{16}.2\sqrt{\dfrac{16xy}{xy}}+\dfrac{31}{16}.4}=\dfrac{4}{33}\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(1;4\right)\)
Đúng 2
Bình luận (0)
a)(3x^2-4)(x+3y) b)(c+3)(x^2+3x) c)(xy-1)(xy+5) d)(3x+5y)(2x-7y) e)-(x-1)(-x^2+2y) f)(-x^2+2y)(x^2+2y)
a: (3x^2-4)(x+3y)
=3x^2*x+3x^2*3y-4x-4*3y
=3x^3+9x^2y-4x-12y
b: (c+3)(x^2+3x)
=c*x^2+c*3x+3x^2+9x
=cx^2+3cx+3x^2+9x
c: (xy-1)(xy+5)
=xy*xy+5xy-xy-5
=x^2y^2+4xy-5
d: (3x+5y)(2x-7y)
=3x*2x-3x*7y+5y*2x-5y*7y
=6x^2-21xy+10xy-35y^2
=6x^2-11xy-35y^2
e: -(x-1)(-x^2+2y)
=(x-1)(x^2-2y)
=x^3-2xy-x^2+2y
f: (-x^2+2y)(x^2+2y)
=(2y)^2-x^4
=4y^2-x^4
Đúng 0
Bình luận (0)
Rút gọn : \(\left(\frac{x-y}{2y-x}-\frac{x^2+y^2+y-2}{x^2-xy-2y^2}\right):\frac{4x^4+4x^2y+y^2-4}{x^2+xy+x+y}:\frac{x+y}{2x^2+y+2}\)
\(=\left(\dfrac{x-y}{2y-x}-\dfrac{x^2+y^2+y-2}{x^2-2xy+xy-2y^2}\right):\dfrac{\left(2x^2+y\right)^2-4}{x\left(x+y\right)+\left(x+y\right)}:\dfrac{x+y}{2x^2+y+2}\)
\(=\left(\dfrac{x-y}{2y-x}-\dfrac{x^2+y^2+y-2}{\left(x-2y\right)\left(x+y\right)}\right)\cdot\dfrac{\left(x+y\right)\left(x+1\right)}{\left(2x^2+y+2\right)\left(2x^2+y-2\right)}\cdot\dfrac{2x^2+y+2}{x+y}\)
\(=\dfrac{y^2-x^2-x^2-y^2-y+2}{\left(x-2y\right)\left(x+y\right)}\cdot\dfrac{x+1}{2x^2+y-2}\)
\(=\dfrac{-\left(2x^2+y-2\right)}{\left(x-2y\right)\left(x+y\right)}\cdot\dfrac{x+1}{2x^2+y-2}=\dfrac{-\left(x+1\right)}{\left(x-2y\right)\left(x+y\right)}\)
Đúng 0
Bình luận (0)