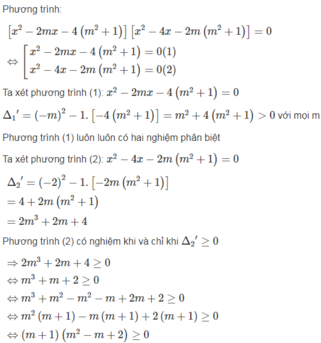tìm m,n để hai phương trình sau có nghiệm chung:
x2+2mx+4=0x2+2mx+4=0 và x2−4x+n=0

Những câu hỏi liên quan
Tìm tất cả các giá trị của tham số mm để phương trình x2−2mx+m2−m+1=0x2−2mx+m2−m+1=0 có hai nghiệm x1,x2 thỏa mãn x2^3−2x1^3+6mx1=19
Câu 1: Cho phương trình: : x2 – 2mx - 10 = 0
a) Giải phương trình khi m = 1
b) Tìm giá trị của tham số m để phương trình x2 – 2mx + 10 = 0 có hai nghiệm phân
biệt \(x1\), \(x2\) thỏa mãn \(x1^2\) + \(x2^2\) = 29
a) Khi \(m=1\) thì pt đã cho trở thành \(x^2-2x-10=0\) (*)
pt (*) có \(\Delta'=\left(-1\right)^2-\left(-10\right)=11>0\)
Do đó (*) có 2 nghiệm phân biệt \(\left[{}\begin{matrix}x_1=\dfrac{-\left(-1\right)+\sqrt{11}}{1}=1+\sqrt{11}\\x_2=\dfrac{-\left(-1\right)-\sqrt{11}}{1}=1-\sqrt{11}\end{matrix}\right.\)
b) Xét pt đã cho \(x^2-mx-10=0\) \(\left(a=1;b=-m;c=-10\right)\)
Nhận thấy \(ac=1\left(-10\right)=-10< 0\) nên pt đã cho luôn có 2 nghiệm phân biệt \(x_1,x_2\).
Áp dụng hệ thức Vi-ét, ta có \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{-m}{1}=m\\x_1x_2=\dfrac{-10}{1}=-10\end{matrix}\right.\)
Ta có \(x_1^2+x_2^2=29\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=29\Leftrightarrow m^2-2\left(-10\right)=29\)\(\Leftrightarrow m^2+20=29\Leftrightarrow m^2=9\Leftrightarrow m=\pm3\)
Vậy để pt đã cho có 2 nghiệm phân biệt thỏa mãn đề bài thì \(m=\pm3\)
Đúng 2
Bình luận (0)
a Tìm m để phương trình vô nghiệm: x2 - (2m - 3)x + m2 = 0.
b Tìm m để phương trình vô nghiệm: (m - 1)x2 - 2mx + m -2 = 0.
c Tìm m để phương trình vô nghiệm: (2 - m)x2 - 2(m + 1)x + 4 - m = 0
\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)
Đúng 0
Bình luận (0)
Cho hai phương trình x 2 – 4x + 4= 0 và x 2 + (m + 1)x + m = 0 . Tìm m để hai phương trình trên có nghiệm chung?
A. m = 2 hoặc m = -1
B. m = 1 hoặc m = 2
C. m = -1
D. m = -2
Đáp án D
* Xét phương trình : x 2 – 4 x + 4 = 0
⇔ ( x - 2 ) 2 = 0 ⇔ x - 2 = 0 ⇔ x = 2
Vậy phương trình này có nghiệm duy nhất.
Để hai phương trình đã cho có nghiệm chung khi và chỉ khi x = 2 là nghiệm phương trình
x 2 + ( m + 1 ) x + m = 0 .Suy ra:
2 2 + ( m + 1 ) . 2 + m = 0
⇔ 4 + 2m + 2 + m = 0 ⇔ 6 + 3m = 0
⇔ 3m = -6 ⇔ m = -2
Đúng 0
Bình luận (0)
Tìm m để phương trình (m + 1)\(x^2\) - 2mx + m + 6 = 0 có hai nghiệm phân biệt x1 và x2 thỏa mãn 0 < x1 <x2
\(\Leftrightarrow\left\{{}\begin{matrix}m+1\ne0\\\Delta'=m^2-\left(m+1\right)\left(m+6\right)>0\\x_1+x_2=\dfrac{2m}{m+1}>0\\x_1x_2=\dfrac{m+6}{m+1}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne1\\-7m-6>0\\\dfrac{2m}{m+1}>0\\\dfrac{m+6}{m+1}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -\dfrac{6}{7}\\\left[{}\begin{matrix}m>0\\m< -1\end{matrix}\right.\\\left[{}\begin{matrix}m>-1\\m< -6\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow m< -6\)
Đúng 2
Bình luận (0)
Cho phương trình ẩn x: x2 – 2mx + 4 = 0 (1)
a) Giải phương trình đã cho khi m = 3.
b) Tìm giá trị của m để phương trình (1) có hai nghiệm x1, x2 thỏa mãn: ( x1 + 1 )2 + ( x2 + 1 )2 = 2.
a, Thay m=3 vào pt ta có:
\(\left(1\right)\Leftrightarrow x^2-6x+4=0\\ \Leftrightarrow x=3\pm\sqrt{5}\)
b, Để pt có 2 nghiệm thì \(\Delta'\ge0\)
\(\Leftrightarrow\left(-m\right)^2-1.4\ge0\\ \Leftrightarrow m^2-4\ge0\\ \Leftrightarrow\left[{}\begin{matrix}m\ge2\\m\le-2\end{matrix}\right.\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=4\end{matrix}\right.\)
\(\left(x_1+1\right)^2+\left(x_2+1\right)^2=2\\ \Leftrightarrow x^2_1+2x_1+1+x^2_2+2x_2+1=2\\ \Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\left(x_1+x_2\right)=0\\ \Leftrightarrow\left(2m\right)^2-2.4+2.2m=0\\ \Leftrightarrow4m^2+4m-8=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\left(ktm\right)\\m=-2\left(tm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho phương trình : x2 + 2mx + 2m - 2 = 0 ( * ) ( x là ẩn số ) . a ) Chứng tỏ phương trình ( * ) luôn có nghiệm x1 , x2 với mọi m . b ) Tìm giá trị tham số m để hai nghiệm x1, x2 của phương trình : ( * ) thỏa mãn : x12 + x22 - 3x1x2 = 4
Xem chi tiết
PT $(*)$ là PT bậc nhất ẩn $x$ thì làm sao mà có $x_1,x_2$ được hả bạn?
PT cuối cũng bị lỗi.
Bạn xem lại đề!
Đúng 0
Bình luận (1)
Lời giải:
a)
Ta có: $\Delta'=m^2-(2m-2)=m^2-2m+2=(m-1)^2+1>0$ với mọi $m\in\mathbb{R}$
Do đó pt luôn có 2 nghiệm phân biệt $x_1,x_2$ với mọi $m\in\mathbb{R}$
b)
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=-2m\\ x_1x_2=2m-2\end{matrix}\right.\)
Để $x_1^2+x_2^2-3x_1x_2=4$
$\Leftrightarrow (x_1+x_2)^2-5x_1x_2=4$
$\Leftrightarrow (-2m)^2-5(2m-2)=4$
$\Leftrightarrow 4m^2-10m+6=0$
$\Leftrightarrow 2m^2-5m+3=0$
$\Leftrightarrow (m-1)(2m-3)=0$
$\Rightarrow m=1$ hoặc $m=\frac{3}{2}$ (đều thỏa mãn)
Đúng 0
Bình luận (0)
(Đề thi học sinh giỏi toán Bulgari - Mùa xuân năm 1997). Tìm giá trị của m để phương trình [
x
2
- 2mx - 4(
m
2
+ 1)][
x
2
- 4x - 2m(
m
2
+1)] 0 có đúng ba nghiệm phân biệt.
Đọc tiếp
(Đề thi học sinh giỏi toán Bulgari - Mùa xuân năm 1997). Tìm giá trị của m để phương trình [ x 2 - 2mx - 4( m 2 + 1)][ x 2 - 4x - 2m( m 2 +1)] = 0 có đúng ba nghiệm phân biệt.
Cho phương trình
x
2
+
2
m
x
-
3
m
+
4
0
. Giả sử phương trình có hai nghiệm x1, x2. Lập phương trình bậc hai có các nghiệm là x12 và x22.
Đọc tiếp
Cho phương trình x 2 + 2 m x - 3 m + 4 = 0 . Giả sử phương trình có hai nghiệm x1, x2. Lập phương trình bậc hai có các nghiệm là x12 và x22.
![]()
![]()
![]()
![]()
Đáp án: D
Theo định lý Vi-ét ta có
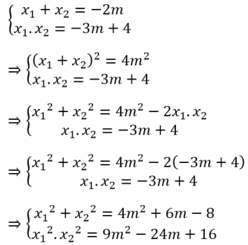
Khi đó, ![]() là nghiệm của phương trình
là nghiệm của phương trình
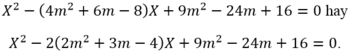
Đúng 0
Bình luận (0)
Cho phương trình (ẩn x) : x 2 – 2mx – 4m – 4 = 0(1)
b) Tìm m để phương trình (1) có 2 nghiệm x 1 , x 2 thỏa mãn x 1 2 + x 2 2 - x 1 x 2 = 13 = 13
b) Gọi x 1 ; x 2 lần lượt là 2 nghiệm của phương trình đã cho
Theo hệ thức Vi-et ta có:
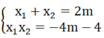
x 1 2 + x 2 2 - x 1 x 2 = x 1 + x 2 2 - 3x1 x2 = 4 m 2 + 3(4m + 4)
Theo bài ra: x 1 2 + x 2 2 - x 1 x 2 =13
⇒ 4m2 + 3(4m + 4) = 13 ⇔ 4m2 + 12m - 1 = 0
∆ m = 122 -4.4.(-1) = 160 ⇒ ∆ m = 4 10
Phương trình có 2 nghiệm phân biệt
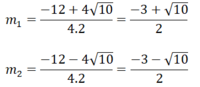
Vậy với 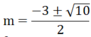 thì phương trình có 2 nghiệm
x
1
;
x
2
thỏa mãn điều kiện
x
1
2
+
x
2
2
-
x
1
x
2
= 13
thì phương trình có 2 nghiệm
x
1
;
x
2
thỏa mãn điều kiện
x
1
2
+
x
2
2
-
x
1
x
2
= 13
Đúng 0
Bình luận (0)