Cho hình chóp SABCD có SA vuông góc với (ABCD) ; đáy ABCD là hình thang vuông tai A và D, AD=DC =a , AB= 2a, SA = a✓3
@) CM CD vuong với (SAD)
B) CM (SAC) vuông voi (SBC)
C) tính góc giua SB và (ABCD) goc giữa SC va (SAB)
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với (ABCD) và SA = 2a. 1. Chứng minh (SCD) vuông góc với (SAD) 2. Tính d(A, (SCD))
1: CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
=>(SCD) vuông góc (SAD)
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a ,SA vuông góc với đáy và SA = a √3 /3. Góc giữa( SBC) và( ABCD) bằng bao nhiêu
\(\left\{{}\begin{matrix}BC\perp SA\subset\left(SAB\right)\\BC\perp AB\subset\left(SAB\right)\end{matrix}\right.\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)
\(\left\{{}\begin{matrix}BC\perp SB\\BC\perp AB\\\left(SBC\right)\cap\left(ABCD\right)=BC\end{matrix}\right.\Rightarrow\left(\left(SBC\right),\left(ABCD\right)\right)=\widehat{SBA}\)
\(\tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{3.a}=\dfrac{\sqrt{3}}{3}\Rightarrow\widehat{SBA}=30^0\)
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, SA = a. Thể tích V của khối chóp SBCD là
A. V = a 3 3
B. V = a 3 6
C. V = a 3 4
D. V = a 3 8
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy, SA = a. Thể tích V của khối chóp SBCD là.
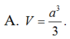
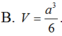
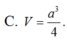

Cho hình chóp SABCD có SA vuông góc với (ABCD), SA=a\(\sqrt{2}\), đáy abcd là hình thang vuông tại A và D với AB=2a, AD=DC=a. Tính góc giữa (SBC) và (ABCD)
Cho hình chóp SABCD có ABCD là hình vuông cạnh a, SA vuông góc với mp (ABCD) SC tạo với mp (ABCD) một góc 45 độ. Gọi E là trung điểm BC. Tính thể tích khối chóp SABCD và khoảng cách giữa hai đường thẳng DE và SC
Cho hình chóp SABCD có SA vuông góc với (ABCD), SA=a√22, đáy abcd là hình thang vuông tại A và D với AB=2a, AD=DC=a. Tính góc giữa (SBC) và (SCD)
Cho hình chóp SABCD có đáy ABCD là hình vuông tâm O cạnh bằng a SA vuông góc với mặt phẳng ABCD SA = a căn 3 gọi alpha là mặt phẳng qua AB và vuông góc với SC T

\(\left\{{}\begin{matrix}BD\perp AC\left(\text{ABCD là hình vuông}\right)\\SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp AC\)
\(\Rightarrow BD\in\left(\alpha\right)\)
Trong mp (SBC), từ B kẻ \(BE\perp SC\Rightarrow E\in\left(\alpha\right)\)
\(\Rightarrow\) Tam giác BDE là thiết diện của chóp và \(\left(\alpha\right)\)
\(BD=AB\sqrt{2}=a\sqrt{2}\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\) hay tam giác SBC vuông tại B
\(SB=\sqrt{SA^2+AB^2}=2a\)
Hệ thức lượng: \(\dfrac{1}{BE^2}=\dfrac{1}{SB^2}+\dfrac{1}{BC^2}-\dfrac{1}{4a^2}+\dfrac{1}{a^2}=\dfrac{5}{4a^2}\Rightarrow BE=DE=\dfrac{2a\sqrt{5}}{5}\)
\(\Rightarrow OE=\sqrt{BE^2-\left(\dfrac{BD}{2}\right)^2}=\dfrac{a\sqrt{30}}{10}\)
\(S_{BDE}=\dfrac{1}{2}OE.BD=\dfrac{a^2\sqrt{15}}{10}\)
Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, S A = a 3 và vuông góc với đáy. Góc giữa đường thẳng SD và mặt phẳng A B C D bằng
A. 60 °
B. 45 °
C. 30 °
D. arcsin 3 5
Đáp án A.
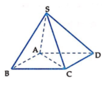
Ta có S A ⊥ ( A B C D ) nên A là hình chiếu của S trên mặt phẳng A B C D . Suy ra AD là hình chiếu của SD trên mặt phẳng A B C D .
Khi đó S D , A B C D ^ = S D , A D ^ = S D A ^ (do S D A ^ < 90 ° ).
Do Δ S A D vuông tại A nên tan S D A ^ = S A A D = a 3 a = 3 ⇒ S D A ^ = 60 ° .
Vậy S D , A B C D ^ = 60 ° .
CHO HÌNH CHÓP SABCD CÓ ĐÁY ABCD LÀ HÌNH CHỮ NHẬT. SA VUÔNG GÓC VỚI ABCD KẺ ĐƯỜNG CAO AM CỦA TAM GIÁC SAB CHỨNG MINH AM VUÔNG GÓC VỚI SBC