Hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng .
Chứng minh rằng AC//BD .
Những câu hỏi liên quan
Hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng. Chứng minh rằng AC//BD
Cách 1:Xét tứ giác ADBC có
AB và CD cắt nhau tại O là trung điểm của mỗi đường
=>ADBC là hình bình hành
=>AC//BD(đl)
Cách 2 Chứng minh được \(\Delta AOC=\Delta BOD\left(AO=OC;\widehat{AOC}=\widehat{BOD};OC=OD\right)\)
\(\Rightarrow\widehat{CAO}=\widehat{DBO}\)Hay \(\widehat{CAB}=\widehat{DBA}\)
Hai góc này ở vị trí so le trong bằng nhau
=> AC//BD
Hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn. Chứng minh rằng AC // BD
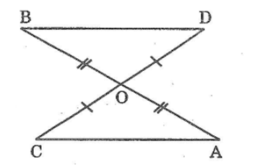
Xét Δ AOC và Δ BOD, ta có:
OA = OB ( Vì O là trung điểm của AB )
∠(AOC) =∠(BOD) (đối đỉnh)
OC = OD ( Vì O là trung điểm của CD)
Suy ra: ΔAOC = ΔBOD (c.g.c)
⇒∠A =∠B (hai góc tương ứng)
Vậy: AC // BD (vì có hai góc so le trong bằng nhau)
Đúng 0
Bình luận (0)
Bài3: Hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng. Chứng minh rằng AC // BD.
Ta có hình vẽ:
Xét Δ AOC và Δ BOD có:
OA = OB (gt)
AOC = BOD (đối đỉnh)
OC = OD (gt)
Do đó, Δ AOC = Δ BOD (c.g.c)
=> ACO = ODB (2 góc tương ứng)
Mà ACO và ODB là 2 góc so le trong nên AC // BD (đpcm)
Đúng 2
Bình luận (3)
Ta có hình vẽ sau:
Xét ΔOAC và ΔOBD có:
OA = OB (gt)
\(\widehat{O_1}\) = \(\widehat{O_2}\) (2 góc đối đỉnh)
OC = OD (gt)
\(\Rightarrow\) ΔOAC = ΔOBD (c.g.c)
\(\Rightarrow\) \(\widehat{C}\) = \(\widehat{D}\) (2 góc tương ứng)
Mà 2 góc này lại ở vị trí so le trong nên
\(\Rightarrow\) AC // BD(đpcm)
Đúng 2
Bình luận (0)
mik ko bt lm
Hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng.
Chứng minh rằng AC // BD ?
Xét \(\Delta AOD\) và \(\Delta BOC\), ta có: AO = BO (vì O là trung điểm của AB); \(\widehat{AOD}=\widehat{BOC}\) (đối đỉnh); OD = OC (vì O là trung điểm của CD)
\(\Rightarrow\Delta AOD=\Delta BOC\left(c-g-c\right)\)
\(\Rightarrow\widehat{DAO}=\widehat{OBC}\) (2 góc tương ứng)
Mà hai góc này ở vị trí so le cho nên AC // BD.
Hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng. Chứng minh rằng AC // BD.
Giúp mk với
TRẢ LỜI:
Xét Δ AOC và Δ BOD, ta có:
OA = OB ( Vì O là trung điểm của AB )
∠(AOC) =∠(BOD) (đối đỉnh)
OC = OD ( Vì O là trung điểm của CD)
Suy ra: ΔAOC = ΔBOD (c.g.c)
⇒∠A =∠B (hai góc tương ứng)
Vậy: AC // BD (vì có hai góc so le trong bằng nhau)
Xét Δ AOC và Δ BOD có:
OA = OB (gt)
AOC = BOD (đối đỉnh)
OC = OD (gt)
Do đó, Δ AOC = Δ BOD (c.g.c)
=> ACO = ODB (2 góc tương ứng)
Mà ACO và ODB là 2 góc so le trong nên AC // BD (đpcm)
K cần vẽ hình cx đc nha
Xem thêm câu trả lời
Hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng. Chứng minh AC//BD
hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng. Chứng minh AC//BD
Bài 12. Cho hai đoạn thẳng AB, CD vuông góc với nhau và cắt nhau tại trung điểm của mỗi đoạn. Chứng minh rằng các đoạn thẳng AC, CB, BD, DA bằng nhau
cho 2 đoạn thẳng AB , CD ⊥ với nhau và cắt nhau tại O là trung điểm của mỗi đoạn , chứng minh AC = BC = BD = DA
Tự vẽ hình.
Do O là trung điểm của AB ➙OA=OB(1)
Do O là trung điểm của DC➙OC=OD(1')
Xét△ACO và △BDO có :
CO=OD(Theo 1')
Góc COA = Góc DOB =90°
AO=OB(Theo 1)
➙△ACO=△BDO (C.G.C)
➙ CA = DB ( hai cạnh tương ứng)(*)
Xét 2 tam giác vuông COB và DOA có
AO=OB (cmt)
CO=OD(cmt)
Góc AOD =góc COB =90°
➙△COB=△DOA ( c.g.c)
➙DA=CB( hai cạnh tương ứng)(**)
Xét △AOC và △BOC có
OC chung
AO=OB (cmt)
➙△AOC=△BOC(c.g.c)
➙AC=CB (***)
Từ (*)(**)(***) suy ra AC=CB=DB=AD (đpcm)
Đúng 1
Bình luận (0)