7846⁷³⁹-7846⁷³⁸

=7846⁷³⁸x7846-7846⁷³⁸

=7846⁷³⁸x(7846-1)

=7846⁷³⁸x7845  \(⋮\)7845

Có:

7846⁷³⁹-7884⁷³⁸

=7846⁷³⁸.7846-7846⁷³⁸.1

=7846⁷³⁸.(7846-1)

=7846⁷³⁸.7845\(⋮7845\)

=>\(7846^{739}-7846^{738}⋮7845\)

tk nha!

Cho : 41087 : X = 3 (dư 2 ). Giá trị của X là: *

1 điểm

a. X = 7846

b. X = 13695

c. X = 1111

Cho : 41087 : X = 3 (dư 2 ). Giá trị của X là: *

1 điểm

a. X = 7846

b. X = 13695

c. X = 1111

đáp án B X=13695

đúng k

hok tốt

 Đap an b

a. \(2\left(a^2+b^2\right)=\left(a-b\right)^2\)

\(\Leftrightarrow2a^2+2b^2=a^2+b^2-2ab\)

\(\Leftrightarrow a^2+b^2=-2ab\)

\(\Leftrightarrow a^2+2ab+b^2=0\)

\(\Leftrightarrow\left(a+b\right)^2=0\)

\(\Leftrightarrow a+b=0\Leftrightarrow a=-b\) (đpcm)

b. \(a^2+b^2+c^2+3=2\left(a+b+c\right)\)

\(\Leftrightarrow a^2+b^2+c^2+3-2a-2b-2c=0\)

\(\Leftrightarrow\left(a^2-2a+1\right)+\left(b^2-2b+1\right)+\left(c^2-2c+1\right)=0\)

\(\Leftrightarrow\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2=0\)

Vì \(\left(a-1\right)^2;\left(b-1\right)^2;\left(c-1\right)^2\ge0\)

\(\Rightarrow\left(a-1\right)^2=\left(b-1\right)^2=\left(c-1\right)^2=0\)

\(\Leftrightarrow a-1=b-1=c-1=0\Leftrightarrow a=b=c=1\)

c. \(\left(a+b+c\right)^2=3\left(ab+bc+ca\right)\)

\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=3\left(ab+bc+ca\right)\)

\(\Leftrightarrow a^2+b^2+c^2=ab+bc+ca\)

\(\Leftrightarrow2\left(a^2+b^2+c^2\right)=2\left(ab+bc+ca\right)\)

\(\Leftrightarrow\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ca+a^2\right)=0\)

\(\Leftrightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)

Tương tự câu b ta có a = b = c

Em thử ạ!Em không chắc đâu.Hơi quá sức em rồi

Ta có: \(VT=\Sigma\frac{x^3}{z+y+yz+1}=\Sigma\frac{x^3}{z+y+\frac{1}{x}+1}\)

\(=\Sigma\frac{x^4}{xz+xy+1+x}=\frac{x^4}{xy+xz+x+1}+\frac{y^4}{yz+xy+y+1}+\frac{z^4}{zx+yz+z+1}\)

Áp dụng BĐT Cauchy-Schwarz dạng Engel,suy ra:

\(VT\ge\frac{\left(x^2+y^2+z^2\right)^2}{\left(x+y+z\right)+2\left(xy+yz+zx\right)+3}\)

\(\ge\frac{\left(\frac{1}{3}\left(x+y+z\right)^2\right)^2}{\left(x+y+z\right)+\frac{2}{3}\left(x+y+z\right)^2+3}\) (áp dụng BĐT \(a^2+b^2+c^2\ge\frac{\left(a+b+c\right)^2}{3};ab+bc+ca\le\frac{\left(a+b+c\right)^2}{3}\))

Đặt \(t=x+y+z\ge3\sqrt{xyz}=3\) Dấu "=" xảy ra khi x = y = z

Ta cần chứng minh: \(\frac{\frac{t^4}{9}}{\frac{2}{3}t^2+t+3}\ge\frac{3}{4}\Leftrightarrow\frac{t^4}{9\left(\frac{2}{3}t^2+t+3\right)}=\frac{t^4}{6t^2+9t+27}\ge\frac{3}{4}\)(\(t\ge3\))

Thật vậy,BĐT tương đương với: \(4t^4\ge18t^2+27t+81\)

\(\Leftrightarrow3t^4-18t^2-27t+t^4-81\ge0\)

Ta có: \(VT\ge3t^4-18t^2-27t+3^4-81\)

\(=3t^4-18t^2-27t\).Cần chứng minh\(3t^4-18t^2-27t\ge0\Leftrightarrow3t^4\ge18t^2+27t\)

Thật vậy,chia hai vế cho \(t\ge3\),ta cần chứng minh \(3t^3\ge18t+27\Leftrightarrow3t^3-18t-27\ge0\)

\(\Leftrightarrow3\left(t^3-27\right)-18\left(t-3\right)\ge0\)

\(\Leftrightarrow\left(t-3\right)\left(3t^2+9t+27\right)-18\left(t-3\right)\ge0\)

\(\Leftrightarrow\left(t-3\right)\left(3t^2+9t+9\right)\ge0\)

BĐT hiển nhiên đúng,do \(t\ge3\) và \(3t^2+9t+9=3\left(t+\frac{3}{2}\right)^2+\frac{9}{4}\ge\frac{9}{4}>0\)

Dấu "=" xảy ra khi t = 3 tức là \(\hept{\begin{cases}x=y=z\\xyz=1\end{cases}}\Leftrightarrow x=y=z=1\)

Chứng minh hoàn tất

Em sửa chút cho bài làm ngắn gọn hơn.

Khúc chứng minh: \(4t^4\ge18t^2+27t+81\)

\(\Leftrightarrow4t^4-18t^2-27t-81\ge0\)

\(\Leftrightarrow\left(t-3\right)\left(4t^3+12t^2+18t+27\right)\ge0\)

BĐT hiển nhiên đúng do \(t\ge3\Rightarrow\hept{\begin{cases}t-3\ge0\\4t^3+12t^2+18t+27>0\end{cases}}\)

Còn khúc sau y chang :P Lúc làm rối quá nên không nghĩ ra ạ!

Áp dụng BĐT cosi ta có

\(\frac{x^3}{\left(1+y\right)\left(1+z\right)}+\frac{1+z}{8}+\frac{1+y}{8}\ge\frac{3}{4}x\)

\(\frac{y^3}{\left(1+x\right)\left(1+z\right)}+\frac{1+x}{8}+\frac{1+z}{8}\ge\frac{3}{4}y\)

\(\frac{z^3}{\left(1+y\right)\left(1+x\right)}+\frac{1+y}{8}+\frac{1+x}{8}\ge\frac{3}{4}z\)

Khi đó 

\(VT\ge\frac{3}{4}\left(x+y+z\right)-\frac{1}{4}\left(x+y+z\right)-\frac{3}{4}=\frac{1}{2}\left(a+b+c\right)-\frac{3}{4}\)

Mà \(x+y+z\ge3\sqrt[3]{xyz}=3\)

=> \(VT\ge\frac{3}{2}-\frac{3}{4}=\frac{3}{4}\)(ĐPCM)

Dấu bằng xảy ra khi x=y=z=1

Theo nguyên lý Dirichlet, trong 3 số \(x^2;y^2;z^2\) luôn có ít nhất 2 số cùng phía so với 1

Không mất tính tổng quát, giả sử đó là \(x^2\) và \(y^2\)

\(\Rightarrow\left(x^2-1\right)\left(y^2-1\right)\ge0\)

\(\Rightarrow x^2y^2\ge x^2+y^2-1\)

\(\Rightarrow x^2y^2+2x^2+2y^2+4\ge x^2+y^2-1+2x^2+2y^2+4\)

\(\Rightarrow\left(x^2+2\right)\left(y^2+2\right)\ge3\left(x^2+y^2+1\right)\)

\(\Rightarrow\left(x^2+2\right)\left(y^2+2\right)\left(z^2+2\right)\ge3\left(x^2+y^2+1\right)\left(1+1+z^2\right)\ge3\left(x+y+z\right)^2\ge9\left(xy+yz+zx\right)\)

Dấu "=" xảy ra khi \(\left(x;y;z\right)=\left(1;1;1\right);\left(-1;-1;-1\right)\)

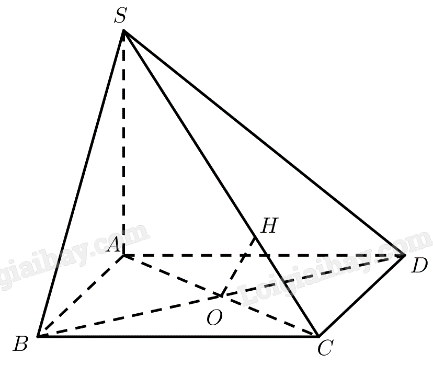
a) \(ABCD\) là hình vuông \( \Rightarrow BC\parallel A{\rm{D}}\)

Mà \(A{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\)

\( \Rightarrow BC\parallel \left( {SAD} \right) \Rightarrow d\left( {BC,\left( {SAD} \right)} \right) = d\left( {B,\left( {SAD} \right)} \right)\)

\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB\)

\(ABCD\) là hình vuông \( \Rightarrow AB \bot A{\rm{D}}\)

\( \Rightarrow AB \bot \left( {SA{\rm{D}}} \right) \Rightarrow d\left( {B,\left( {SA{\rm{D}}} \right)} \right) = AB = a\)

Vậy \(d\left( {BC,\left( {SAD} \right)} \right) = a\).

b) \(ABCD\) là hình vuông \( \Rightarrow B{\rm{D}} \bot A{\rm{C}}\)

\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot B{\rm{D}}\)

\( \Rightarrow B{\rm{D}} \bot \left( {SAC} \right)\)

Gọi \(O = AC \cap B{\rm{D}}\), kẻ \(OH \bot SC\left( {H \in SC} \right)\)

\(B{\rm{D}} \bot \left( {SAC} \right) \Rightarrow B{\rm{D}} \bot OH\)

\( \Rightarrow d\left( {B{\rm{D}},SC} \right) = OH\)

\(\Delta ABC\) vuông tại \(B\)\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}}  = a\sqrt 2  \Rightarrow OC = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)

\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\) vuông tại \(A\)\( \Rightarrow SC = \sqrt {S{A^2} + A{C^2}}  = a\sqrt 3 \)

\(\Delta SAC \backsim \Delta OHC\,(g.g) \Rightarrow \frac{{SA}}{{OH}} = \frac{{SC}}{{OC}} \Rightarrow OH = \frac{{SA.OC}}{{SC}} = \frac{{a\sqrt 6 }}{6}\)

Vậy \(d\left( {B{\rm{D}},SC} \right) = \frac{{a\sqrt 6 }}{6}\).

a: Nếu a chẵn, b chẵn thì ab(a+b)=2k*2c*(2k+2c)=4kc(2k+2c) chia hết cho 2

Nếu a,b ko cùng tính chẵn lẻ thì 

ab(a+b)=2k(2c+1)(2k+2c+1) chia hết cho 2

Nếu a,b lẻ thì (a+b) chia hết cho 2

=>ab(a+b) chia hết cho 2

b: \(\overline{ab}-\overline{ba}=10a+b-10b-a=9a-9b=9\left(a-b\right)⋮9\)