câu b ạ

Những câu hỏi liên quan
giúp mình cái này với ạ!:< ở câu b ý ạ câu a em giải rồi ạ!
Câu d thôi ạ, câu a, b, c làm rồi ạ
Cho mình hỏi câu nào mới là câu đúng ạ\(Cho mình hỏi câu B có đúng ko ạ\)
Chọn B là đúng rồi em
Đúng 2
Bình luận (0)
Mong các bạn giải giúp mình câu b với ạ! ( câu b mình làm không đúng đâu )
Còn câu a là thầy giáo mình đã chữa.
Cảm ơn các bạn nhiều ạ !!!


hơi mờ ạ, làm câu a trc nhé, lát em đăng lại thì làm câu b ạ
a: góc yAt'=180 độ-60 độ=120 độ
góc yAt'=góc yOx
mà hai góc này đồng vị
nên At'//Ox
b: góc mOA=góc xOy/2=60 độ
góc nAO=góc OAt/2=60 độ
=>góc mOA=góc nAO
=>Om//An
Đúng 1
Bình luận (0)
Ai giúp mình câu b phần 2 bài III với cả câu b bài IV với ạ. Mình xin cảm ơn rất rất nhiều ạ.

Bài III.2b.
Phương trình hoành độ giao điểm của \(\left(P\right)\) và \(\left(d\right)\) : \(x^2=\left(m+1\right)x-m-4\)
hay : \(x^2-\left(m+1\right)x+m+4=0\left(I\right)\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm nên phương trình \(\left(I\right)\) sẽ có hai nghiệm phân biệt. Do đó, phương trình \(\left(I\right)\) phải có :
\(\Delta=b^2-4ac=\left[-\left(m+1\right)\right]^2-4.1.\left(m+4\right)\)
\(=m^2+2m+1-4m-16\)
\(=m^2-2m-15>0\).
\(\Rightarrow m< -3\) hoặc \(m>5\).
Theo đề bài : \(\sqrt{x_1}+\sqrt{x_2}=2\sqrt{3}\)
\(\Rightarrow\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=\left(2\sqrt{3}\right)^2=12\)
\(\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=12\left(II\right)\)
Do phương trình \(\left(I\right)\) có hai nghiệm khi \(m< -3\) hoặc \(m>5\) nên theo định lí Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m+1\right)}{1}=m+1\\x_1x_2=\dfrac{c}{a}=\dfrac{m+4}{1}=m+4\end{matrix}\right.\).
Thay vào \(\left(II\right)\) ta được : \(m+1+2\sqrt{m+4}=12\)
Đặt \(t=\sqrt{m+4}\left(t\ge0\right)\), viết lại phương trình trên thành : \(t^2-3+2t=12\)
\(\Leftrightarrow t^2+2t-15=0\left(III\right)\).
Phương trình \(\left(III\right)\) có : \(\Delta'=b'^2-ac=1^2-1.\left(-15\right)=16>0\).
Suy ra, \(\left(III\right)\) có hai nghiệm phân biệt :
\(\left\{{}\begin{matrix}t_1=\dfrac{-b'+\sqrt{\Delta'}}{a}=\dfrac{-1+\sqrt{16}}{1}=3\left(t/m\right)\\t_2=\dfrac{-b'-\sqrt{\Delta'}}{a}=\dfrac{-1-\sqrt{16}}{1}=-5\left(ktm\right)\end{matrix}\right.\)
Suy ra được : \(\sqrt{m+4}=3\Rightarrow m=5\left(ktm\right)\).
Vậy : Không có giá trị m thỏa mãn đề bài.
Đúng 3
Bình luận (0)
Bài IV.b.
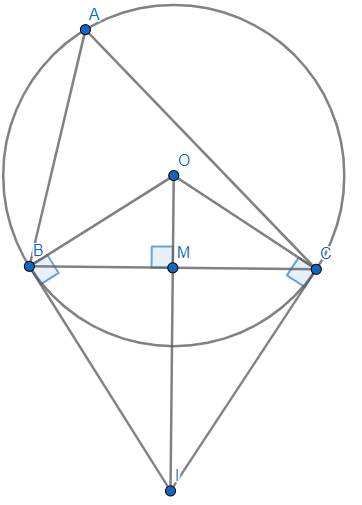
Chứng minh : Ta có : \(OB=OC=R\) nên \(O\) nằm trên đường trung trực \(d\) của \(BC\).
Theo tính chất hai tiếp tuyến cắt nhau thì \(IB=IC\), suy ra \(I\in d\).
Suy ra được \(OI\) là một phần của đường trung trực \(d\) của \(BC\) \(\Rightarrow OI\perp BC\) tại \(M\) và \(MB=MC\).
Xét \(\Delta OBI\) vuông tại \(B\) có : \(MB^2=OM.OI\).
Lại có : \(BC=MB+MC=2MB\)
\(\Rightarrow BC^2=4MB^2=4OM.OI\left(đpcm\right).\)
Tính diện tích hình quạt tròn
Ta có : \(\hat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\Rightarrow sđ\stackrel\frown{BC}=2.\hat{BAC}=2.70^o=140^o\) (góc nội tiếp).
\(\Rightarrow S=\dfrac{\pi R^2n}{360}=\dfrac{\pi R^2.140^o}{360}=\dfrac{7}{18}\pi R^2\left(đvdt\right)\)
Đúng 2
Bình luận (0)
câu a,b thôi ạ gaapspppppppppppppppppppppppppppppp ạ
a,theo giả thiết E lần lượt là hình chiếu của H lên AB,
H là chân đường vuông góc kẻ từ B xuống AC
\(=>\)\(\angle\left(BEH\right)=\angle\left(BHA\right)=90^o\)
có \(\angle\left(B\right)chung\)\(=>\Delta BEH\sim\Delta BHA\left(g.g\right)\left(dpcm\right)\)
b, ta có E,F là hình chiếu của H trên AB,BC
\(=>HE\perp AB,HF\perp BC\)
mà \(BH\perp AC\left(gt\right)=>\)\(\Delta BHA\) vuông tại H có HE là đường cao
và \(\Delta BHC\) vuông tại H có HF là đường cao
theo hệ thức lượng
\(=>BH^2=BE.BA=BF.BC\left(dpcm\right)\)
Đúng 1
Bình luận (0)
Mn giải thích giúp e với ạ.
Tại sao câu a và câu b lại làm như thế ạ?

Bạn chỉ cần áp dụng cái phân tích đa thức thành nhân tử bằng phương pháo đặt nhân tử chung là ra rồi
Đúng 0
Bình luận (1)
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
Đọc tiếp
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Đúng 4
Bình luận (0)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
Đúng 1
Bình luận (0)
giúp mình câu b với ạ. cảm mơn ạ
a: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH^2=4\cdot9=36\)
=>AH=6(cm)
BC=BH+CH
=4+9
=13(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{4\cdot13}=2\sqrt{13}\left(cm\right)\\AC=\sqrt{9\cdot13}=3\sqrt{13}\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có \(tanABC=\dfrac{AC}{AB}=\dfrac{3}{2}\)
nên \(\widehat{ABC}\simeq56^0\)
b: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>AH=EF
Xét ΔHAB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\)
Xét ΔHAC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\)
\(AE\cdot AB+AF\cdot AC=AH^2+AH^2=2AH^2=2FE^2\)
Đúng 1
Bình luận (0)

























