Cho hai hàm số:
f(x) = 2x+1 và g(x) = -x+3
Tìm x để f(x) = g(x)
#Giúp mình vs nha!
cho hàm số f(x)=2x+1; G(x)=1-2x
a) tính f(g(x)) và g(f(x))
b) tìm x sao cho f(x)=g(x)
Cho hai hàm số y= f(x) và y= g(x) . Hai hàm số y= f’(x) và g’(x) có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y= g’(x).
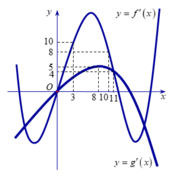
Hàm số h(x)=f(x+4)-g(2x-32) đồng biến trên khoảng nào dưới đây?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
a) Cho hàm số y=f(x)=-2x+3.Tính f(-2);f(-1);f(0);f(-1/2);f(1/2)
b) Cho hàm số y=g(x)=x^2-1.Tính g(-1);g(0);g(1);g(2)
c)Với giá trị nào của x để hai hàm số trên nhận cùng giá trị
Làm bài c thôi ạ mấy câu còn lại nháp thôi ạ.
cho hai hàm số : f(x) = x^2 và g(x) = 3 - x .
a) Tính f(-3) , f(-1/2) , f(0) , g(1) , g(2) , g(3) .
b) Xác định a để 2f(a) = g(a) .
\(a,f\left(-3\right)=9;f\left(-\dfrac{1}{2}\right)=\dfrac{1}{4};f\left(0\right)=0\\ g\left(1\right)=2;g\left(2\right)=1;g\left(3\right)=0\\ b,2f\left(a\right)=g\left(a\right)\\ \Leftrightarrow2a^2=3-a\\ \Leftrightarrow2a^2+a-3=0\\ \Leftrightarrow2a^2-2a+3a-3=0\\ \Leftrightarrow2a\left(a-1\right)+3\left(a-1\right)=0\\ \Leftrightarrow\left(2a+3\right)\left(a-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=1\\a=-\dfrac{3}{2}\end{matrix}\right.\)
Cho hai hàm số f(x)=x+2 và g ( x ) = x 2 - 2 x + 3 Đạo hàm của hàm số y = g f x tại x=1 bằng
A. 4
B. 1
C. 3
D. 2
Cho hai hàm số: f(x)=|x-1|+1 và g(x)=|x-2|+2.
1. Tìm x để f(x)-2g(x)=-3
2. Tìm x để f(x)=g(f(2))
Thay vào:
|x−1|+1−2[|x−2|+2]=−3|x−1|+1−2[|x−2|+2]=−3
⇔|x−1|−2|x−2|=−3−1+4=0⇔⇔|x−1|−2|x−2|=−3−1+4=0⇔
|x−1|−2|x−2|=0|x−1|−2|x−2|=0(1)
Chia khoảng ⎧⎩⎨⎪⎪x<1|x−1|=1−x|x−2|=2−x{x<1|x−1|=1−x|x−2|=2−x⇒(1)⇔1−x−4+2x=0⇒x=3>1⇒(1)⇔1−x−4+2x=0⇒x=3>1(LOẠI)
⎧⎩⎨⎪⎪1≤x<2|x−1|=x−1|x−2|=2−x{1≤x<2|x−1|=x−1|x−2|=2−x⇒x−1−4+2x=0⇒x=53<2⇒x−1−4+2x=0⇒x=53<2(NHẬN)
⎧⎩⎨⎪⎪x≥2|x−1|=x−1|x−2|=x−2{x≥2|x−1|=x−1|x−2|=x−2⇒x−1+4−2x=0⇒x=3>2⇒x−1+4−2x=0⇒x=3>2(nhận)
Kết luận: ⎡⎣x=53x=3
Cho hàm số f(x) = x^2 - 2x +1 và g(x) = f(sin2x) , đạo hàm của hamf số g(x) là?
\(f'\left(x\right)=2x-2\)
\(g'\left(x\right)=2cos2x.f'\left(sin2x\right)=2cos2x.\left(2sin2x-2\right)=4cos2x\left(sin2x-1\right)\)
Cho hai hàm số y = f(x) = x+1 và y = g(x) = x+ \(\sqrt{\frac{4}{25}}\). Tìm giá trị x của hàm số y = f(x) để f(x) = g(0)
\(\hept{\begin{cases}f\left(x\right)=x+1\\g\left(x\right)=x+\sqrt{\frac{4}{25}}=x+\frac{2}{5}\end{cases}}\)
\(g\left(0\right)=\frac{2}{5}\Rightarrow f\left(x\right)=\frac{2}{5}\Rightarrow x+1=\frac{2}{5}\Rightarrow x=-\frac{3}{5}\)
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) = 0, F(2) = 1, G(2) = 1 và ∫ 0 2 F ( x ) g ( x ) d x = 3 . Tính tích phân hàm: ∫ 0 2 G ( x ) f ( x ) d x
A. I = 3.
B. I = 0.
C. I = -2.
D. I = -4.
Chọn C.
Đặt u = G ( x ) d v = f ( x ) d x ⇒ d u = G ( x ) ' d x = g ( x ) d x v = ∫ f ( x ) d x = F ( x )
Suy ra: I = G ( x ) F ( x ) 2 0 - ∫ 0 2 F ( x ) g ( x ) d x
= G(2)F(2) – G(0)F(0) – 3 = 1 – 0 – 3 = -2.