Tìm x biết: ( 72x2 -18x + 1)( 12x2 - 7x + 1) = 5

Những câu hỏi liên quan
Tìm x, biết: ( 72x2 - 18x + 1)( 12x2 - 7x + 1)
tìm x biết (72x^2-18x+1)(12x^2-7x+10=5
Với mỗi phương trình sau, đã biết một nghiệm (ghi kèm theo), hãy tìm nghiệm kia:
a
)
12
x
2
−
8
x
+
1
0
;
x
1...
Đọc tiếp
Với mỗi phương trình sau, đã biết một nghiệm (ghi kèm theo), hãy tìm nghiệm kia:
a ) 12 x 2 − 8 x + 1 = 0 ; x 1 = 1 2 b ) 2 x 2 − 7 x − 39 = 0 ; x 1 = − 3 c ) x 2 + x − 2 + 2 = 0 ; x 1 = − 2 d ) x 2 − 2 m x + m − 1 = 0 ; x 1 = 2
Theo định lý Vi-et ta có: phương trình
a
x
2
+
b
x
+
c
= 0 có hai nghiệm
x
1
;
x
2
thì: 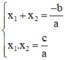
Ta sử dụng một trong hai biểu thức trên để tìm nghiệm còn lại.
Ở bài giải dưới đây ta sẽ sử dụng điều kiện: 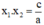
(Các bạn có thể làm cách 2 sử dụng điều kiện 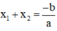 ).
).
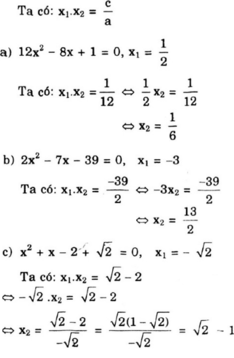
d) x 2 - 2 m x + m - 1 = 0 ( 1 )
Vì x 1 = 2 là một nghiệm của pt (1) nên:
2 2 - 2 m . 2 + m - 1 = 0
⇔ 4- 4 m+ m – 1 = 0
⇔ 3- 3m = 0
⇔ m = 1
Khi m = 1 ta có: x 1 . x 2 = m - 1 (hệ thức Vi-ét)
⇔ 2 . x 2 = 0 ( v ì x 1 = 2 và m = 1)
⇔ x 2 = 0
Đúng 0
Bình luận (0)
Bài 1. (2,0 điểm) Cho đa thức A(x) = –11x^5 + 4x – 12x2 + 11x^5+ 13x^2– 7x + 2.
a) Thu gọn, sắp xếp đa thức A(x) theo số mũ giảm dần của biến rồi tìm bậc, hệ số cao nhất của đa thức.
A(x)= (11x5 - 11x5) + (13x2 - 12x2) - (7x - 4x) + 2 = x2 - 3x + 2
Bậc đa thức: Đa thức bậc 2
Hệ số bậc cao nhất (ít ai hỏi hệ số cao nhất lắm): 1
Đúng 1
Bình luận (0)
a) \(A\left(x\right)=-11x^5+4x-12x^2+11x^5+13x^2-7x+2\)
\(=x^2-3x+2\)
Đa thức \(A\left(x\right)\) có bậc là \(2\), hệ số cao nhất của đa thức là \(1\)
Đúng 1
Bình luận (2)
a) \(-11x^5+4x-12x^2+11x^5+13x^2-7x+2\)
\(=\left(-11x^5+11x^5\right)-\left(12x^2-13x^2\right)+\left(4x-7x\right)+2\)
\(=-\left(-x^2\right)+\left(-3x\right)+2\)
\(=x^2-3x+2\)
Vậy bậc của đa thức là 2
Hệ số cao nhất là 1
Đúng 0
Bình luận (0)
Câu 1
Rút gọn các biểu thức sau:
a. 2x(3x + 2) - 3x(2x + 3)
b. (x + 2)3 + (x - 3)2 - x2(x + 5)
c. (3x3 - 4x2 + 6x) : 3x
Câu 2
Phân tích đa thức sau thành nhân tử: 2x3 - 12x2 + 18x
Câu 3
Tìm x, biết: 3x(x - 5) - x2 + 25 0
Câu 4 Cho hình bình hành ABCD (AB AD). Gọi E và K lần lượt là trung điểm của CD và AB. BD cắt AE, AC, CK lần lượt tại N, O và I. Chứng minh rằng:
a. Tứ giắc AECK là hình bình hành.
b. Ba điểm E, O, K thẳng hàng.
c. DN NI IB
d. AE...
Đọc tiếp
Câu 1
Rút gọn các biểu thức sau:
a. 2x(3x + 2) - 3x(2x + 3)
b. (x + 2)3 + (x - 3)2 - x2(x + 5)
c. (3x3 - 4x2 + 6x) : 3x
Câu 2
Phân tích đa thức sau thành nhân tử: 2x3 - 12x2 + 18x
Câu 3
Tìm x, biết: 3x(x - 5) - x2 + 25 = 0
Câu 4 Cho hình bình hành ABCD (AB > AD). Gọi E và K lần lượt là trung điểm của CD và AB. BD cắt AE, AC, CK lần lượt tại N, O và I. Chứng minh rằng:
a. Tứ giắc AECK là hình bình hành.
b. Ba điểm E, O, K thẳng hàng.
c. DN = NI = IB
d. AE = 3KI
Câu 5 Cho x, y là hai số thực tùy ý, tìm giá trị nhỏ nhất của biểu thức sau:
P = x2 + 5y2 + 4xy + 6x + 16y + 32
Câu 1:
a) 2x(3x+2) - 3x(2x+3) = 6x^2+4x - 6x^2-9x = -5x
b) \(\left(x+2\right)^3+\left(x-3\right)^2-x^2\left(x+5\right)\)
\(=x^3+6x^2+12x+8+x^2-6x+9-x^3-5x^2\)
\(=2x^2+6x+17\)
c) \(\left(3x^3-4x^2+6x\right)\div\left(3x\right)=x^2-\dfrac{4}{3}x+2\)
Đúng 2
Bình luận (0)
Câu 2:
\(2x^3-12x^2+18x=2x\left(x^2-6x+9\right)=2x\left(x^2-2.x.3+3^2\right)=2x\left(x-3\right)^2\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 1: Thực hiện phép tính
a/ 5x2y (x2y– 4xy2 + 7xy)
b/ 3xy2 (x2y3 + x 2y – xy2 )
c/ 3x(12x2 + 4x – 5) + 2x(9x2 – 6x + 7)
d/ 5x(2x2 – 9x – 5) – 9x (x2 - 7x – 4)
a/ 5x2y (x2y– 4xy2 + 7xy)
`=5x^4y^2-20x^3y^3+35x^3y^2`
b/ 3xy2 (x2y3 + x 2y – xy2 )
`=3x^3y^5+3x^3y^3-3x^2y^4`
c/ 3x(12x2 + 4x – 5) + 2x(9x2 – 6x + 7)
`=36x^3+12x^2-15x+18x^3-18x^2+14x`
`=54x^3-6x^2-x`
d/ 5x(2x2 – 9x – 5) – 9x (x2 - 7x – 4)
`=10x^3-45x^2-25x-9x^3+63x^2+36x`
`=x^3+18x^2+11x`
Đúng 3
Bình luận (0)
Phân tích đa thức thành nhân tử
1) 2x3–x2+5x+3
2) 27x3−27x2+18x–427x3−27x2+18x–4
3) x2+2xy+y2−x−y–12x2+2xy+y2−x−y–12
4) (x+2)(x+3)(x+4)(x+5)–24(x+2)(x+3)(x+4)(x+5)–24
5) 4x4−32x2+14x4−32x2+1
6) 3(x4+x2+1)−(x2+x+1)23(x4+x2+1)−(x2+x+1)2
7) 64x4+y4
Tìm x biết
(
2
x
4
–
3
x
3
+
x
2
)
:
-
1
2
x
2
+
4
(
x...
Đọc tiếp
Tìm x biết ( 2 x 4 – 3 x 3 + x 2 ) : - 1 2 x 2 + 4 ( x – 1 ) 2 = 0
A. x = -1
B. x = 2
C. x = 1
D. x = 0
Ta có
( 2 x 4 – 3 x 3 + x 2 ) : - 1 2 x 2 + 4 ( x – 1 ) 2 = 0 ⇔ 2 x 4 : ( - 1 2 x 2 ) - 3 x 3 : ( - 1 2 x 2 ) + x 2 : ( - 1 2 x 2 ) + 4 ( x 2 - 2 x + 1 ) = 0 ⇔ - 4 x 2 + 6 x – 2 + 4 x 2 – 8 x + 4 = 0
ó -2x + 2 = 0
ó x = 1
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)
a. (2x⁵-5x³+x²+3x-1):(x²-1) b. (5x⁵-2x⁴-9x³+7x²-18x-3):(x²-3)
a: \(=\dfrac{2x^5-2x^3-3x^3+3x+x^2-1}{x^2-1}\)
\(=2x^3-3x+1\)
Đúng 0
Bình luận (0)






















