
giúp mìn câu này với , mìn cảm ơn rất nhiều
Giúp mìn bài này với ạ mìn cảm ơn 
Mn giải giúp mình câu 2 vs ạ. Mìn cảm ơn nhiều
Đk:\(y^2-2x-5y+6\ge0\)
Pt (1)\(\Leftrightarrow\left(x^2-1\right)-\left(xy-y\right)+\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)-y\left(x-1\right)+\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2-y\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\y=x+2\end{matrix}\right.\)
TH1: Thay x=1 vào pt (2) ta đc: \(3\sqrt{y^2-5y+4}=y+9\)
\(\Leftrightarrow\left\{{}\begin{matrix}y+9\ge0\\9\left(x^2-5y+4\right)=y^2+18y+81\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y\ge-9\\8y^2-63y-45=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}y=\dfrac{63+3\sqrt{601}}{16}\\y=\dfrac{63-3\sqrt{601}}{16}\end{matrix}\right.\) (tm)
TH2: Thay y=x+2 vào pt (2) ta đc:
\(\left(x-1\right)^2+3\sqrt{\left(x+2\right)^2-2x-5\left(x+2\right)+6}=x+2+9\)
\(\Leftrightarrow x^2-3x-10+3\sqrt{x^2-3x}=0\)
Đặt \(t=\sqrt{x^2-3x}\left(t\ge0\right)\)
Pttt: \(t^2-10+3t=0\)\(\Leftrightarrow\left[{}\begin{matrix}t=2\left(tm\right)\\t=-5\left(ktm\right)\end{matrix}\right.\)
\(\Rightarrow2=\sqrt{x^2-3x}\)\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-1\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}y=6\\y=1\end{matrix}\right.\) (tm)
Vậy \(\left(x;y\right)=\text{}\left\{\left(1;\dfrac{63+3\sqrt{601}}{16}\right);\left(1;\dfrac{63-3\sqrt{601}}{16}\right),\left(4;6\right),\left(-1;1\right)\right\}\)
Xét pt đầu:
\(\left(x^2+x-2\right)-y\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)-y\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2-y\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\y=x+2\end{matrix}\right.\)
- Với \(x=1\) thay xuống pt dưới:
\(3\sqrt{y^2-5y+4}=y+9\) \(\left(y\ge-9\right)\)
\(\Leftrightarrow9\left(y^2-5y+4\right)=y^2+18y+81\)
\(\Leftrightarrow8y^2-63y-45=0\)
\(\Rightarrow y=\dfrac{63\pm3\sqrt{601}}{16}\) (thỏa mãn)
- Với \(y=x+2\) thay xuống pt dưới:
\(\left(x-1\right)^2+3\sqrt{x^2-3x}=x+11\) (ĐKXĐ: ....)
\(\Leftrightarrow x^2-3x+3\sqrt{x^2-3x}-10=0\)
Đặt \(\sqrt{x^2-3x}=t\ge0\)
\(\Rightarrow t^2+3t-10=0\Rightarrow\left[{}\begin{matrix}t=2\\t=-5\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{x^2-3x}=2\Leftrightarrow x^2-3x-4=0\)
\(\Leftrightarrow...\)
Giúp mình bài này với mìn cảm ơn 
Gọi giá ban đầu của đôi giày nếu không khuyến mãi là x(vnđ)
Giá tiền được giảm là: 65%x(vnđ)
Theo đề bài ra ta có:
x-65%x=1 520 000
<=>35%x=1 520 000
<=> x=4 342 857,143
x=4 342 857,143
Vậy giá tiền ban đầu của chiếc giày là 4 342 857,143
Mọi người giúp mình bài này với mìn cảm ơn
Mọi người giúp mìn cách làm bài này với . Cảm ơn mọi người ạ .
Có bạn nào biết làm câu nàyt hì giúp mình nha mìn đang cần gấp trước 5giowf nếu được thì mình cảm ơn nhiều
Rewrite sentences:
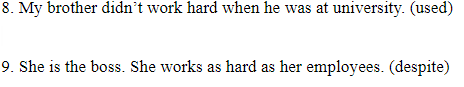
My brother didn't use to work hard when he was in university.
Despite being the boss, she works as hard as her employees.
Giúp mình với mình cần gấp🥰 mìn cảm ơn
1.\(sin^2\alpha+cos^2\alpha=\left(\dfrac{AC}{BC}\right)^2+\left(\dfrac{AB}{BC}\right)^2\)
=\(\dfrac{AC^2+AB^2}{BC^2}=\dfrac{BC^2\left(pytago\right)}{BC^2}=1\)
2.ta có \(tan\alpha=\dfrac{AC}{AB}\)
\(\dfrac{sin\alpha}{cos\alpha}=\dfrac{\dfrac{AC}{BC}}{\dfrac{AB}{BC}}=\dfrac{AC}{AB}\)
\(\Rightarrow tan\alpha=\dfrac{sin\alpha}{cos\alpha}\)
3.ta có:\(1+tan^2\alpha=1+\left(\dfrac{sin\alpha}{cos\alpha}\right)^2\)
=\(\dfrac{sin^2\alpha+cos^2\alpha}{cos^2\alpha}\)=\(\dfrac{1}{cos^2\alpha}\)
4.ta có :\(cot\alpha=\dfrac{AB}{AC}\)
\(\dfrac{cos\alpha}{sin\alpha}=\dfrac{\dfrac{AB}{BC}}{\dfrac{AC}{BC}}=\dfrac{AB}{AC}\)
\(\Rightarrow cot\alpha=\dfrac{cos\alpha}{sin\alpha}\)
\(1+cot^2\alpha=1+\left(\dfrac{cos\alpha}{sin\alpha}\right)^2=\dfrac{sin^2\alpha+cos^2\alpha}{sin^2\alpha}\)=\(\dfrac{1}{sin^2a}\)
Tìm số nguyên x biết: A)x+2=-8 B)(x+2)^3-2=25 C)2^x.2^x+1=2^15 Giúp mìn với mìn cảm ơn trc:((
Tìm GTNN hoặc GTLN :\(C=\left(2\text{x}^2+3\right)^2-7\)
Các bạn nhớ giúp mìn bài này nha !
Cảm ơn các bạn nhiều .
Ta có:(2x\(^2\)+3) luôn lớn hơn hoặc bằng 0 với mọi x
=>(2x\(^2\)+3)\(^2\) -7 luôn lớn hơn hoặc bằng -7 với mọi x
Vậy GTNN của biểu thức C là 7
Dấu "=" xảy ra khi (2x\(^2\)+3)\(^2\)=0
=>2x\(^2\)+3 =0
2x\(^2\) =-3
x\(^2\) =\(\frac{-3}{2}\)
x =\(\sqrt{\left(\frac{-3}{2}\right)^2}\)
Vậy GTNN của biểu thức C là -7 khi x=\(\sqrt{\left(\frac{-3}{2}\right)^2}\)
GTNN : ta co : (2x2+3)2 luôn lớn hơn hoặc bằng 0
=> để C đạt giá trị nhỏ nhất thì (2x2+3)2 =0
=> C =0-7=-7
Sai hết rùi kìa .... !!!!
Mình giải đúng nè !!!!
Ta có :
\(2x^2\ge0\forall x\)
\(\Leftrightarrow2x^2+3\ge3\forall x\)
\(\Leftrightarrow\left(2x^2+3\right)^2\ge3^2=9\forall x\)
\(\Rightarrow\left(2x^2+3\right)^2-7\ge9-7=2\forall x\) Có GTNN là 2 tại x = 0
Vật GTNN của C là 2 tại x = 0