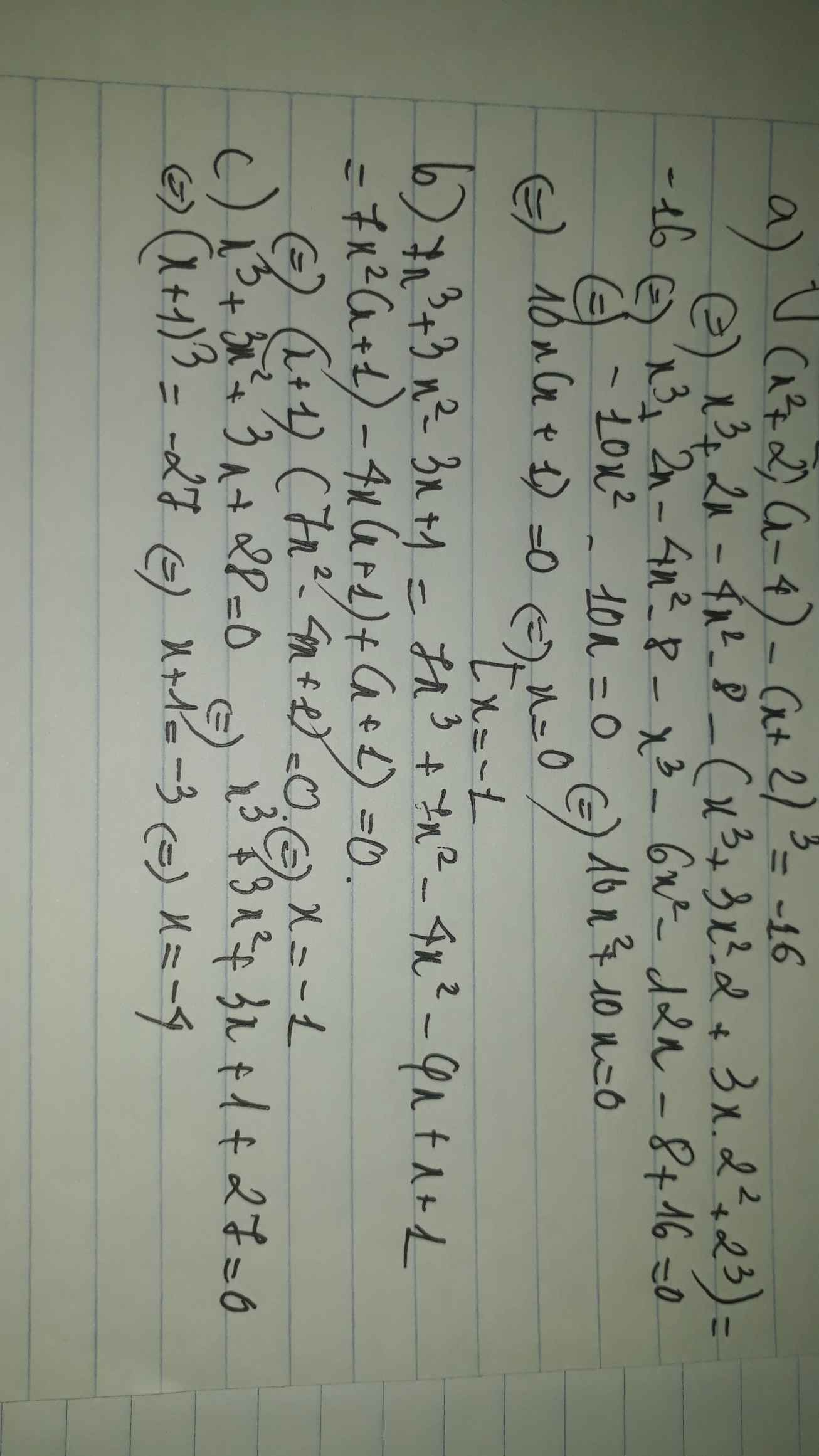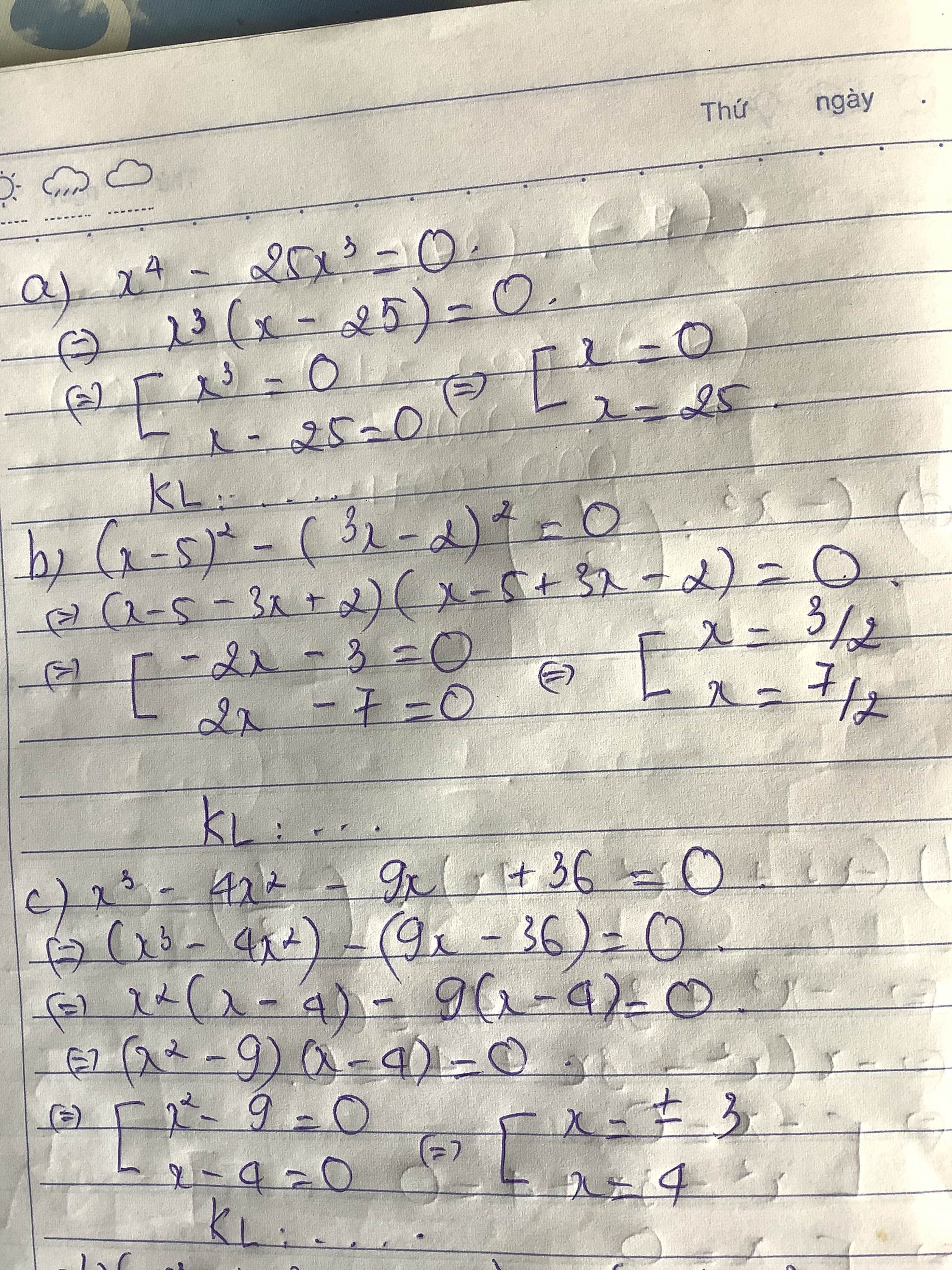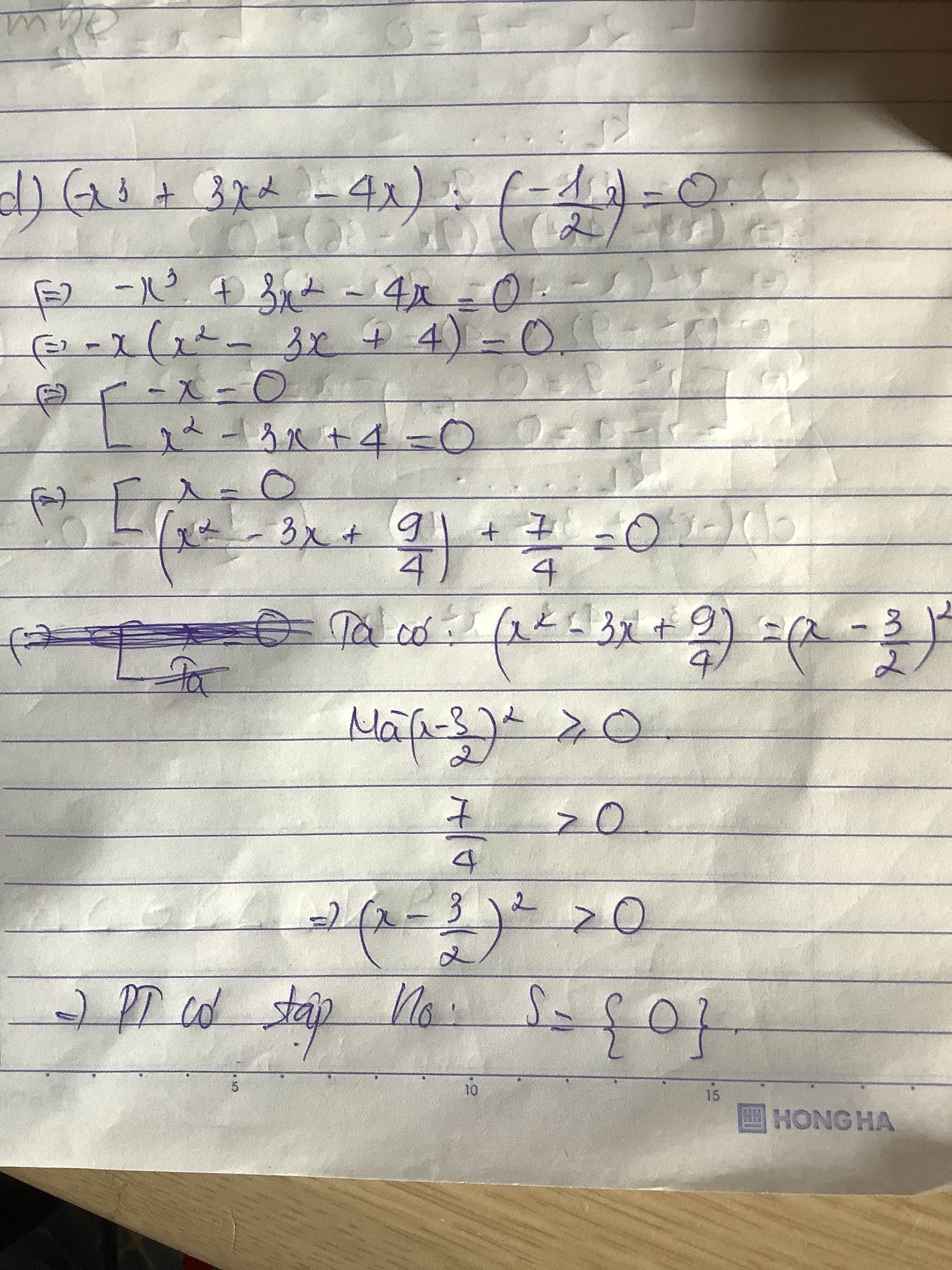Ta có

x 3   +   3 x 2   +   3 x   +   1   =   0   ⇔   ( x   +   1 ) 3   =   0

ó x + 1 = 0 ó x = -1

Vậy x = -1

Đáp án cần chọn là: A

a: Ta có: \(\left(x^2+2\right)\left(x-4\right)-\left(x+2\right)^3=-16\)

\(\Leftrightarrow x^3-4x^2+2x-8-x^3-6x^2-12x-8=-16\)

\(\Leftrightarrow-10x^2-10x=0\)

\(\Leftrightarrow-10x\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\)

c: Ta có: \(x^3+3x^2+3x+28=0\)

\(\Leftrightarrow\left(x+1\right)^3=-27\)

\(\Leftrightarrow x+1=-3\)

hay x=-4

y = x3 – 3x2 + 2.

⇒ y’ = (x3 – 3x2 + 2)’

      = (x3)’ – (3x2)’ + (2)’

      = 3x2 – 3.2x + 0

      = 3x2 – 6x.

y’ > 0

⇔ 3x2 – 6x > 0

⇔ 3x(x – 2) > 0

⇔ x < 0 hoặc x > 2.

a.

$x^4-25x^3=0$

$\Leftrightarrow x^3(x-25)=0$

\(\Leftrightarrow \left[\begin{matrix} x^3=0\\ x-25=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=0\\ x=25\end{matrix}\right.\)

b.

$(x-5)^2-(3x-2)^2=0$

$\Leftrightarrow (x-5-3x+2)(x-5+3x-2)=0$

$\Leftrightarrow (-2x-3)(4x-7)=0$
\(\Leftrightarrow \left[\begin{matrix} -2x-3=0\\ 4x-7=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=\frac{-3}{2}\\ x=\frac{7}{4}\end{matrix}\right.\)

c.

$x^3-4x^2-9x+36=0$

$\Leftrightarrow x^2(x-4)-9(x-4)=0$

$\Leftrightarrow (x-4)(x^2-9)=0$

$\Leftrightarrow (x-4)(x-3)(x+3)=0$

\(\Leftrightarrow \left[\begin{matrix} x-4=0\\ x-3=0\\ x+3=0\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=4\\ x=3\\ x=-3\end{matrix}\right.\)

d. ĐK: $x\neq 0$

$(-x^3+3x^2-4x):(\frac{-1}{2}x)=0$

$\Leftrightarrow x(-x^2+3x-4):(\frac{-1}{2}x)=0$

$\Leftrightarrow -2(-x^2+3x-4)=0$

$\Leftrightarrow x^2-3x+4=0$

$\Leftrightarrow (x-1,5)^2=-1,75< 0$ (vô lý)

Vậy pt vô nghiệm.

x3+3x2-10x=0

=>x(3+3.2-10)=0

=>x=0

x3-5x2-14x=0

=>x(3-5.2-14)=0

=>x=0

x3+5x2-24x=0

=>x(3+5.2-24)=0

=>x=0

Câu a)

\(x^3+3x^2-10=0\Rightarrow x\left(x^2+3x-10\right)=0\Rightarrow x\left(x^2-2x+5x-10\right)=0\Rightarrow x\left(x\left(x-2\right)+5\left(x-2\right)\right)=0\Rightarrow x\left(x+5\right)\left(x-2\right)=0\)

\(\Rightarrow x=0;x=5;x=2\)

Câu b:

\(x^3-5x^2-14x=0\Rightarrow x\left(x^2-5x-14\right)=0\Rightarrow x\left(x^2+2x-7x-14\right)=0\Rightarrow x\left(x\left(x+2\right)-7\left(x+2\right)\right)=0\Rightarrow x\left(x-7\right)\left(x+2\right)=0\)

\(\Rightarrow x=0;x=7;x=-2\)

`P(x)=\(4x^2+x^3-2x+3-x-x^3+3x-2x^2\)

`= (x^3-x^3)+(4x^2-2x^2)+(-2x-x+3x)+3`

`= 2x^2+3`

`Q(x)=`\(3x^2-3x+2-x^3+2x-x^2\)

`= -x^3+(3x^2-x^2)+(-3x+2x)+2`

`= -x^3+2x^2-x+2`

`P(x)-Q(x)-R(x)=0`

`-> P(X)-Q(x)=R(x)`

`-> R(x)=P(x)-Q(x)`

`-> R(x)=(2x^2+3)-(-x^3+2x^2-x+2)`

`-> R(x)=2x^2+3+x^3-2x^2+x-2`

`= x^3+(2x^2-2x^2)+x+(3-2)`

`= x^3+x+1`

`@`\(\text{dn inactive.}\)

a: P(x)-Q(x)-R(x)=0

=>R(x)=P(x)-Q(x)

=2x^2+3+x^3-2x^2+x-2

=x^3+x+1

a: \(C=x^3-3x^2+3x+2023\)

\(C=x^3-3x^2+3x-1+2024\)

\(=\left(x-1\right)^3+2024\)

Khi x=101 thì \(C=\left(101-1\right)^3+2024\)

\(=100^3+2024\)

\(=1000000+2024=1002024\)

b: \(D=x^3-6x^2+12x-100\)

\(=x^3-6x^2+12x-8-92\)

\(=\left(x-2\right)^3-92\)

Khi x=-98 thì \(D=\left(-98-2\right)^3-92\)

\(=-100^3-92\)

\(=-1000000-92=-1000092\)

\(a,PT\Leftrightarrow x^3-6x^2+12x-8-x^3+x+6x^2-18x-10=0\)

\(\Leftrightarrow-5x-18=0\)

\(\Leftrightarrow x=-\dfrac{18}{5}\)

Vậy ...

\(b,PT\Leftrightarrow x^3+3x^2+3x+1-x^3+3x^2-3x+1-6x^2+12x-6+10=0\)

\(\Leftrightarrow12x+6=0\)

\(\Leftrightarrow x=-\dfrac{1}{2}\)

Vậy ...

\(c,PT\Leftrightarrow\left(x+1\right)^3+3^3=0\)

\(\Leftrightarrow\left(x+1+3\right)\left(x^2+2x+1-3x-3+9\right)=0\)

\(\Leftrightarrow\left(x+4\right)\left(x^2-x+7\right)=0\)

Thấy : \(x^2-\dfrac{2.x.1}{2}+\dfrac{1}{4}+\dfrac{27}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{27}{4}\ge\dfrac{27}{4}>0\)

\(\Rightarrow x+4=0\)

\(\Leftrightarrow x=-4\)

Vậy ...

\(d,PT\Leftrightarrow\left(x-2\right)^3+1^3=0\)

\(\Leftrightarrow\left(x-2+1\right)\left(x^2-4x+4-x+2+1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x^2-5x+7\right)=0\)

Thấy : \(x^2-5x+7=x^2-\dfrac{5.x.2}{2}+\dfrac{25}{4}+\dfrac{3}{4}=\left(x-\dfrac{5}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}>0\)

\(\Rightarrow x-1=0\)

\(\Leftrightarrow x=1\)

Vậy ...