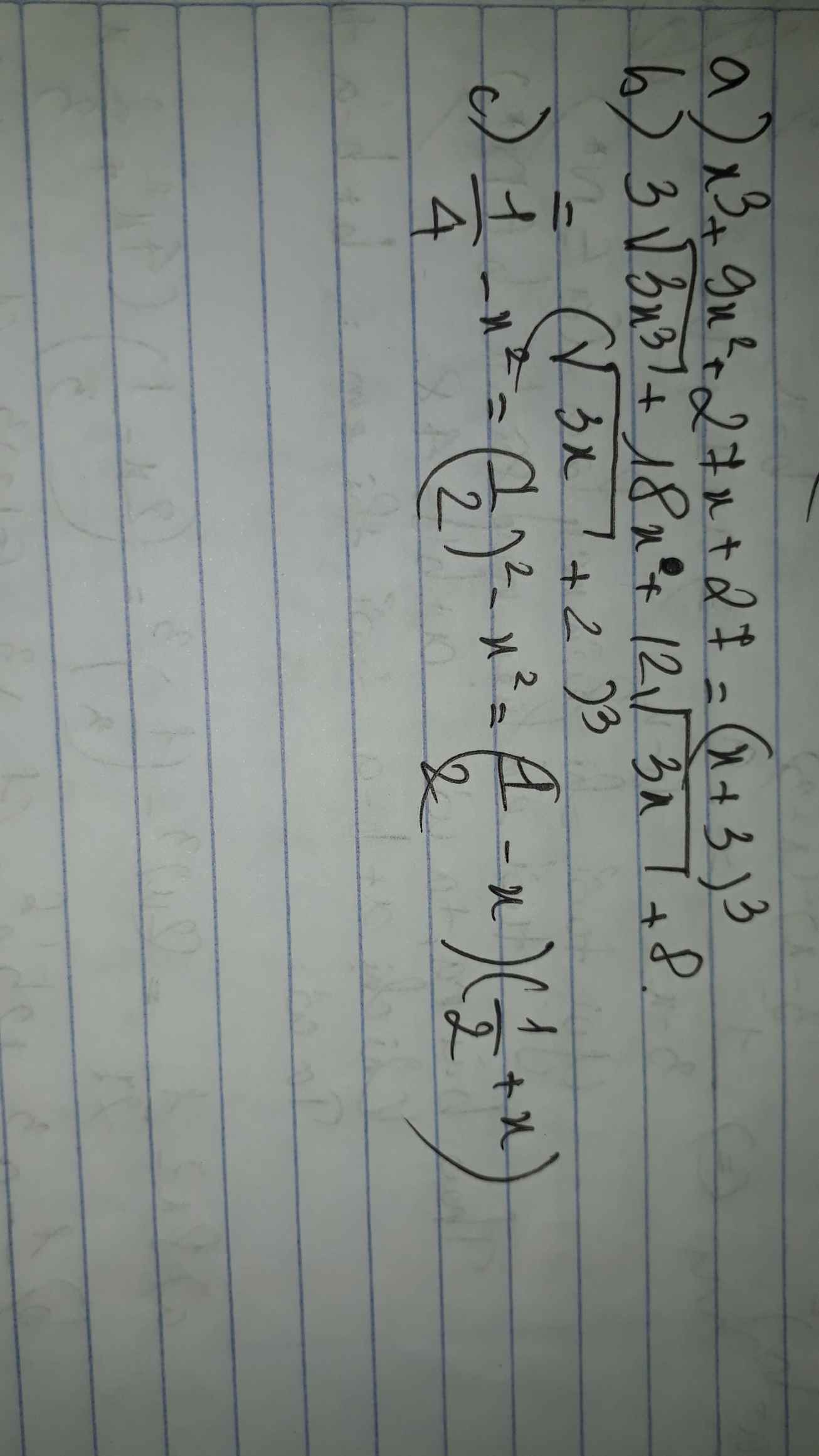Phân tích đa thức thành nhân tử: \(M=7\sqrt{x-1}-\sqrt{x^3-x^2}+x-1\) với \(x\ge1\)

Những câu hỏi liên quan
Phân tích đa thức thành nhân tử:
\(y=7\sqrt{x-1}+x-1-\sqrt{x^3-x^2}\) với \(x\ge1\)
\(y=7\sqrt{x-1}+x-1-\sqrt{x^3-x^2}=7\sqrt{x-1}+x-1-x\sqrt{x-1}=\sqrt{x-1}\left(\sqrt{x-1}-x+7\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cách phân tích đa thức có dạng ax + b\(\sqrt{x}\) + c thành nhân tử với x > 0
từ đó phân tích đa thức x +8 \(\sqrt{x}\) + 7 thành nhân tử với x > 0
phân tích đa thức thành nhân tử
\(x+2\sqrt{x-1}\) (với x≥1)
\(x-4\sqrt{x-2}+2\) ( với x ≥2)
\(x+2\sqrt{x-1}=\left(x-1\right)+2\sqrt{x-1}+1=\left(\sqrt{x-1}+1\right)^2\)
\(x-4\sqrt{x-2}+2=\left(x-2\right)-4\sqrt{x-2}+4=\left(\sqrt{x-2}-2\right)^2\)
Đúng 1
Bình luận (0)
\(x+2\sqrt{x-1}=\left(\sqrt{x-1}+1\right)^2\)
\(x-4\sqrt{x-2}+2=\left(\sqrt{x-2}+4\right)^2\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử:
M= 7\(\sqrt{x-1}\) - \(\sqrt{x^3-x^2}\)+ x -1 với x\(\ge\)1
Ta có : \(M=7\sqrt{x-1}-\sqrt{x^3-x^2}+x-1\)
\(=7\sqrt{x-1}-\sqrt{x^2\left(x-1\right)}+x-1\)
\(=7\sqrt{x-1}-x\sqrt{x-1}+\left(\sqrt{x-1}\right)^2\)
\(=\sqrt{x-1}\left(7-x+\sqrt{x-1}\right)\)
\(=\sqrt{x-1}\left(\sqrt{x-1}+2\right)\left(\sqrt{x-1}-3\right)\)
Đúng 0
Bình luận (1)
phân tích đa thức thành nhân tử
1/\(\frac{x-\sqrt{x}-7}{\sqrt{x}+3}\)
2/\(\frac{x+2\sqrt{x}}{x-2\sqrt{x}}\)
b2 phân tích đa thức thành nhân tử
1) x - 9
2) x - 16
3) 9x - 1
4) x\(\sqrt{x}\)+ 1
1: \(x-9=\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)\)
2: \(x-16=\left(\sqrt{x}-4\right)\left(\sqrt{x}+4\right)\)
3: \(9x-1=\left(3\sqrt{x}-1\right)\left(3\sqrt{x}+1\right)\)
4: \(x\sqrt{x}+1=\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)\)
Đúng 1
Bình luận (0)
\(1,x-9=\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)\\ 2,x-16=\left(\sqrt{x}-4\right)\left(\sqrt{x}+4\right)\\ 3,9x-1=\left(3\sqrt{x}-1\right)\left(3\sqrt{x}+1\right)\\ 4,x\sqrt{x}+1=\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)\)
Đúng 1
Bình luận (0)
1,x−9=(√x−3)(√x+3)
2,x−16=(√x−4)(√x+4)
3,9x−1=(3√x−1)(3√x+1)
4,x√x+1=(√x+1)(x−√x+1
tick nha thanks
Đúng 2
Bình luận (0)
phân tích đa thức thành nhân tử
\(x\sqrt{x}-5\)
\(x+7\sqrt{x}+10\)
\(x+7\sqrt{x}+10=\left(\sqrt{x}+2\right)\left(\sqrt{x}+5\right)\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử
x^3+9x^2+27x+27
3\(\sqrt{3x^3}\)+18x^2+12\(\sqrt{3x}\)+8
\(\dfrac{1}{4}\)-x^2
a) \(x^3+9x^2+27x+27=\left(x+3\right)^3\)
b) \(3\sqrt{3x^3}+18x^2+12\sqrt{3x}+8=\left(\sqrt{3x}+2\right)^3\)
c) \(\dfrac{1}{4}-x^2=\left(\dfrac{1}{2}-x\right)\left(\dfrac{1}{2}+x\right)\)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử (với a b x y không âm, a> b)
a) xy - \(y\sqrt{x}\) + \(\sqrt{x}-1\)
b) \(\sqrt{ab}-\sqrt{by}+\sqrt{bx}+\sqrt{ay}\)
c) \(\sqrt{a+b}+\sqrt{a^2+b^2}\)
d) 12 - \(\sqrt{x}\) - x
d: \(=-\left(x+\sqrt{x}-12\right)=-\left(\sqrt{x}+4\right)\left(\sqrt{x}-3\right)\)
Đúng 0
Bình luận (0)