bài toán chứng minh 2 số tự nhiên là nguyên tố cùng nhau cả ví dụ nhé

Những câu hỏi liên quan
1: viết các công thức về luỹ thừa với số mũ tự nhiên. Cho ví dụ2: So sánh tính chất cơ bản của phép cộng và phép nhân số tự nhiên, số nguyên, phân số3: Với điều kiện nào thì hiệu của hai số tự nhiên cũng là số tự nhiên? Hiệu của hai số nguyên cũng là số nguyên? cho ví dụ4:Với điều kiện nào thì thương của hai số tự nhiên cũng là số tự nhiên? Thương của hai phân số cũng là phân số? Cho ví dụ5:Phát biểu ba bài toán cơ bản về phân số. Cho ví dụ minh hoạ6: Phát biểu các dấu hiệu chia hết cho 2,3,5,9N...
Đọc tiếp
1: viết các công thức về luỹ thừa với số mũ tự nhiên. Cho ví dụ
2: So sánh tính chất cơ bản của phép cộng và phép nhân số tự nhiên, số nguyên, phân số
3: Với điều kiện nào thì hiệu của hai số tự nhiên cũng là số tự nhiên? Hiệu của hai số nguyên cũng là số nguyên? cho ví dụ
4:Với điều kiện nào thì thương của hai số tự nhiên cũng là số tự nhiên? Thương của hai phân số cũng là phân số? Cho ví dụ
5:Phát biểu ba bài toán cơ bản về phân số. Cho ví dụ minh hoạ
6: Phát biểu các dấu hiệu chia hết cho 2,3,5,9
Những số như thế nào thì chia hết cho cả 2 và 5? Cho ví dụ.
Những số như thế nào thi chia hết cho cả 2,3,5 và 9? Cho ví dụ
7: Trong định nghĩa số nguyên và hợp số, có điểm nào giống nhau, điểm nào khác nhau? Tích của hai số nguyên tố là 1 số nguyên tố hay hợp số?
Giải hộ mình nha, cảm ơn nhiều
mình kô pit. Chúc bạn may mắn lần sau nhaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaâ
Đúng 0
Bình luận (0)
Hix làm ơn đi mà ai giúp đi. Sắp nộp rùi huhu
Đúng 0
Bình luận (0)
1. Lũy thừa với số mũ tự nhiên. Có 2 công thức:
+ Nhân hai lũy thừa cùng cơ số: am. an= am+n
VD: 2. 23= 21+3= 24= 16.
+ Chia hai lũy thừa cùng cơ số: am: an= am-n
VD: 26: 23= 26-3= 23= 8.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1, Viết các công thức về lũy thừa với số mũ tự nhiên. Cho ví dụ.2, So sánh tính chất cơ bản của phép cộng và phép nhân số tự nhiên, số nguyên, phân số.3, Với điều kiện nào nào thì hiệu của 2 số tự nhieencungx là stn ? Hiệu của 2 số nguyên cũng là số nguyên ? Cho ví dụ.4, Với điều kiện nào thì thương của 2 số tự nhiên cũng là số tự nhiên ? Thương của 2 phân số cũng là phân số ? Cho ví dụ.5, Phát biểu 3 bài toán cơ bản về phân số. Cho ví dụ minh họa.6, Trong định nghĩa số nguyên tố và hợp số, có đ...
Đọc tiếp
1, Viết các công thức về lũy thừa với số mũ tự nhiên. Cho ví dụ.
2, So sánh tính chất cơ bản của phép cộng và phép nhân số tự nhiên, số nguyên, phân số.
3, Với điều kiện nào nào thì hiệu của 2 số tự nhieencungx là stn ? Hiệu của 2 số nguyên cũng là số nguyên ? Cho ví dụ.
4, Với điều kiện nào thì thương của 2 số tự nhiên cũng là số tự nhiên ? Thương của 2 phân số cũng là phân số ? Cho ví dụ.
5, Phát biểu 3 bài toán cơ bản về phân số. Cho ví dụ minh họa.
6, Trong định nghĩa số nguyên tố và hợp số, có điểm nào giống nhau, điểm nào khác nhau ? Tích của 2 số nguyên toos là một số nguyên tố hay hợp số ?
Bài toán 1 : Chứng minh rằng mọi số nguyên tố p ta có thể tìm được một số được viết bởi hai chữ số chia hết cho p.Bài toán 2 : Chứng minh rằng nếu một số tự nhiên không chia hết cho 2 và 5 thì tồn tại bội của nó có dạng : 111...1.Bài toán 3 : Chứng minh rằng tồn tại số có dạng 1997k (k thuộc N) có tận cùng là 0001.Bài toán 4 : Chứng minh rằng nếu các số nguyên m và n nguyên tố cùng nhau thì tìm được số tự nhiên k sao cho mk - 1 chia hết cho n
Đọc tiếp
Bài toán 1 : Chứng minh rằng mọi số nguyên tố p ta có thể tìm được một số được viết bởi hai chữ số chia hết cho p.
Bài toán 2 : Chứng minh rằng nếu một số tự nhiên không chia hết cho 2 và 5 thì tồn tại bội của nó có dạng : 111...1.
Bài toán 3 : Chứng minh rằng tồn tại số có dạng 1997k (k thuộc N) có tận cùng là 0001.
Bài toán 4 : Chứng minh rằng nếu các số nguyên m và n nguyên tố cùng nhau thì tìm được số tự nhiên k sao cho mk - 1 chia hết cho n
Bài 3: Viết chương trình in ra tất cả các cặp số nguyên tố cách nhau 2 đơn vị và nhỏ hơn 10000. Ví dụ các cặp số nguyên tố đầu tiên cách nhau 2 đơn vị là (3,5), (5,7), (11,13).
Bài 4: Viết chương trình nhập 3 số tự nhiên từ bàn phím là day, month và year có ý nghĩa là ngày, tháng, năm tương ứng. Kiểm tra xem bộ dữ liệu đã nhập có hợp lý hay không. python
Bài 3:
uses crt;
var i:integer;
{------------------chuong-trinh-con-kiem-tra-so-nguyen-to----------------------}
function ktnt(x:integer):boolean;
var kt:boolean;
i:integer;
begin
kt:=true;
for i:=2 to x-1 do
if x mod i=0 then kt:=false;
if kt=true then ktnt:=true
else ktnt:=false;
end;
{-------------------------chuong-trinh-chinh----------------------------}
begin
clrscr;
for i:=2 to 9999 do
if (ktnt(i)=true) and (ktnt(i+2)=true) then
begin
writeln(i,',',i+2);
delay(500);
end;
readln;
end.
Đúng 1
Bình luận (0)
Bài 4:
uses crt;
var a,b,c,kt:integer;
begin
clrscr;
write('Nhap ngay:'); readln(a);
write('Nhap thang:'); readln(b);
write('Nhap nam:'); readln(c);
kt:=0;
if (b=1) and (0<a) and (a<=31) then kt:=1;
if (b=2) and (0<a) and (a<=28) then kt:=1;
if (b=2) and (0<a) and (a<=29) and (c mod 4=0) then kt:=1;
if (b=3) and (0<a) and (a<=31) then kt:=1;
if (b=4) and (0<a) and (a<=30) then kt:=1;
if (b=5) and (0<a) and (a<=31) then kt:=1;
if (b=6) and (0<a) and (a<=30) then kt:=1;
if (b=7) and (0<a) and (a<=31) then kt:=1;
if (b=8) and (0<a) and (a<=31) then kt:=1;
if (b=9) and (0<a) and (a<=30) then kt:=1;
if (b=10) and (0<a) and (a<=31) then kt:=1;
if (b=11) and (0<a) and (a<=30) then kt:=1;
if (b=12) and (0<a) and (a<=31) then kt:=1;
if kt=0 then writeln('Khong hop le')
else writeln('Hop le');
readln;
end.
Đúng 0
Bình luận (0)
Bạn ơi bạn làm ra bài 3 chưa, cho mình xin cách làm nữa.
Python
Đúng 0
Bình luận (0)
câu 3 so sánh tính chất cơ bản của phép cộng và phép nhân số tự nhiên , số nguyên , phân sốcâu 4 với điều kiện nào thì hiệu hai số tự nhiên cũng là số tự nhiên hiệu của hai số nguyên cũng bằng hai số nguyên . cho ví dụcâu 5 với điệu kiện nào thì thương của hai số tự nhiên cũng là hai số tự nhiên, thương của hai phân số cũng là phân số . cho ví dụcâu 6 phát biểu ba bài toán cơ bản về phân số. cho ví dụ minh họacâu 8 trong định nghĩa số nguyên tố và hợp tố có điểm gì giống và khác nhau . tích của...
Đọc tiếp
câu 3 so sánh tính chất cơ bản của phép cộng và phép nhân số tự nhiên , số nguyên , phân số
câu 4 với điều kiện nào thì hiệu hai số tự nhiên cũng là số tự nhiên hiệu của hai số nguyên cũng bằng hai số nguyên . cho ví dụ
câu 5 với điệu kiện nào thì thương của hai số tự nhiên cũng là hai số tự nhiên, thương của hai phân số cũng là phân số . cho ví dụ
câu 6 phát biểu ba bài toán cơ bản về phân số. cho ví dụ minh họa
câu 8 trong định nghĩa số nguyên tố và hợp tố có điểm gì giống và khác nhau . tích của hai số nguyên là một số nguyên hay hợp số
giúp mình giải nha tại mai mình cần gấp
Bài 4. (4 điểm): Hai số tự nhiên được gọi là Nguyên tố tương đương nếu chúng có chung các ước
số nguyên tố. Ví dụ các số 75 và 15 là nguyên tố tương đương vì cùng có các ước nguyên tố là 3
và 5. Cho trước hai số tự nhiên N, M. Hãy viết chương trình kiểm tra xem các số này có là
nguyên tố tương đương với nhau hay không.
uses crt;
var i,n,m,k,d:integer;
{---------------chuong-trinh-con-tim-ucln--------------------}
function ucln(x,y:integer):integer;
var t:integer;
begin
while y<>0 do
begin
t:=x mod y;
x:=y;
y:=t;
end;
ucln:=x;
end;
{------------chuong-trinh-con-kiem-tra-so-nguyen-to-------------------}
function nt(b:longint):boolean;
var j:longint;
begin
nt:=true;
if (b=2) or (b=3) then exit;
nt:=false;
if (b=1) or (b mod 2=0) or (b mod 3=0) then exit;
j:=5;
while j<=trunc(sqrt(b)) do
begin
if (b mod j=0) or (b mod (j+2)=0) then exit;
j:=j+6;
end;
nt:=true;
end;
{---------------chuong-trinh-chinh---------------------}
begin
clrscr;
write('Nhap N: '); readln(N);
write('Nhap M: '); readln(M);
d:=0;
k:=ucln(N,M);
for i:=1 to k do
if nt(i) then d:=d+1;
if d>0 then writeln('2 so nay tuong duong voi nhau')
else writeln('2 so nay khong tuong duong voi nhau');
readln;
end.
Đúng 0
Bình luận (1)
uses crt;
var i,n,m:integer;
a,b:array[1..100]of integer;
function nt(n:integer):boolean;
begin
if n<2 then nt:=false;
for i:=2 to n div 2 do
if n mod i=0 then nt:=false;
end;
function nttd(n,m:integer):boolean;
var i,j,k,d,dem,s:integer;
a,b:array[1..100]of integer;
begin
nttd:=false;
d:=0;
for j:=1 to n do
if (nt(j))and(n mod j=0) then
begin
inc(d);
a[d]:=j;
end;
dem:=0;
for k:=1 to n do
if (nt(k))and(m mod k=0) then
begin
inc(dem);
b[dem]:=k;
end;
s:=0;
if d=dem then for i:=1 to d do if a[i]=b[i] then
inc(s);
if s=d then nttd:=true else nttd:=false;
end;
BEGIN
clrscr;
write('nhap n,m:');readln(n,m);
if nttd(n,m) then writeln(n,' va ',m,' la nguyen to tuong duong')
else writeln(n,' va ',m,' khong phai la nguyen to tuong duong');
readln;
END.
Đúng 0
Bình luận (0)
uses crt;
Var M,N,d,i,luun,luum:integer;
Function USCLN(m,n: integer): integer;
Var r: integer;
Begin
luun:=n;luum:=m;
While n<>0 do
begin
r:=m mod n; m:=n; n:=r;
end;
USCLN:=m;
End;
function nttd:integer;
begin
d:=USCLN(M,N); i:=2;
While d<>1 do
begin
If d mod i =0 then
begin
While d mod i=0 do d:=d div i;
While M mod i=0 do M:=M div i;
While N mod i=0 do N:=N div i;
end;
Inc(i);
end;
If M*N=1 then Write(luum,' va ', luun,' la so nguyen to tuong duong.')
Else Write(luum ,' va ',luun ,' khong phai la so nguyen to tuong duong.');
end;
BEGIN
clrscr;
Write('Nhap M,N:'); Readln(M,N);
nttd;
Readln;
END.
Đúng 0
Bình luận (0)
1.Chứng minh rằng: Với mọi số tự nhiên các số sau là các số nguyên tố cùng nhau.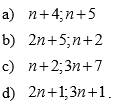
2.Tìm các số tự nhiên để các số sau nguyên tố cùng nhau. 
1:
a: Gọi d=ƯCLN(n+5;n+4)
=>\(\left\{{}\begin{matrix}n+5⋮d\\n+4⋮d\end{matrix}\right.\)
=>\(n+5-n-4⋮d\)
=>\(1⋮d\)
=>d=1
=>n+4 và n+5 là hai số nguyên tố cùng nhau
b: Gọi d=ƯCLN(2n+5;n+2)
=>\(\left\{{}\begin{matrix}2n+5⋮d\\n+2⋮d\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2n+5⋮d\\2n+4⋮d\end{matrix}\right.\)
=>\(2n+5-2n-4⋮d\)
=>\(1⋮d\)
=>d=1
=>2n+5 và n+2 là hai số nguyên tố cùng nhau
c: Gọi d=ƯCLN(3n+7;n+2)
=>\(\left\{{}\begin{matrix}3n+7⋮d\\n+2⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3n+7⋮d\\3n+6⋮d\end{matrix}\right.\)
=>\(3n+7-3n-6⋮d\)
=>\(1⋮d\)
=>d=1
=>3n+7 và n+2 là hai số nguyên tố cùng nhau
d: Gọi d=ƯCLN(2n+1;3n+1)
=>\(\left\{{}\begin{matrix}2n+1⋮d\\3n+1⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6n+3⋮d\\6n+2⋮d\end{matrix}\right.\)
=>\(6n+3-6n-2⋮d\)
=>\(1⋮d\)
=>d=1
=>2n+1 và 3n+1 là hai số nguyên tố cùng nhau
Đúng 2
Bình luận (0)
a) Gọi d là ƯCLN của n + 4 và n + 5
⇒ n + 4 ⋮ d và n + 5 ⋮ d
⇒ (n + 5 - n - 4) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy n + 4 và n + 5 luôn là cặp SNT cùng nhau
b) Gọi d là ƯCLN của 2n + 5 và n + 2
⇒ 2n + 5 ⋮ d và n + 2 ⋮ d
⇒ 2n + 5 ⋮ d và 2(n + 2) ⋮ d
⇒ (2n + 5 - 2n - 4) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy 2n + 5 và n + 2 luôn là cặp SNT cùng nhau
c) Gọi d là ƯCLN của n + 2 và 3n + 7
⇒ n + 2 ⋮ d và 3n + 7 ⋮ d
⇒ 3(n + 2) ⋮ d và 3n + 7 ⋮ d
⇒ (3n + 7 - 3n - 6) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy n + 2 và 3n + 7 luôn là cặp SNT cùng nhau
d) Gọi d là ƯCLN của 2n + 1 và 3n + 1
⇒ 2n + 1 ⋮ d và 3n + 1 ⋮ d
⇒ 3(2n + 1) ⋮ d và 2(3n + 1) ⋮ d
⇒ (6n + 3 - 6n - 2) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy 2n + 1 và 3n + 1 luôn là cặp SNT cùng nhau
Đúng 1
Bình luận (0)
Mấy bài này khó quá,bạn nào giải được mình xin cảm ơn nha :
Bài 1 : Cho a là số tự nhiên lẻ, b là một số tự nhiên. Chứng minh rằng các số:
a) a và ab+4 là 2 số nguyên tố cùng nhau
b)Tìm n để n+2 và 3n+11 là 2 số nguyên tố cùng nhau (n là số tự nhiên)
Bài 2: Chứng minh rằng : S=1+3+5+.........+ (2n-1) (n thuộc N*) là số chính phương .
1. Nhận xét rằng a là số tự nhiên lẻ và ab + 4 là một số chẵn.
Nếu d là một ước chung của a và ab + 4 ( d > 1), thì do a lẻ nên d phải là số lẻ.
Do ab chia hết cho d nên 4 chia hết cho d, suy ra d \(\in\) { 2; 4 }. (mâu thuẫn)..
b) Gọi d là ước chung lớn nhất của n + 2 và 3n + 11.
Suy ra \(\hept{\begin{cases}n+2⋮d\\3n+11⋮d\end{cases}\Rightarrow\hept{\begin{cases}3n+6⋮d\\3n+11⋮d\end{cases}}}\).
Suy ra \(3n+11-\left(3n+6\right)=5⋮d\).
Vì vậy d = 1 hoặc d = 5.
Để n + 2 và 3n + 11 là hai số nguyên tố cùng nhau thì d = 1.
Nếu giả sử ngược lại \(\hept{\begin{cases}n+2⋮5\\3n+11⋮5\end{cases}}\) \(\Leftrightarrow n+2⋮5\).
Suy ra \(n\) chia 5 dư 3 hay n = 5k + 3.
Vậy để n + 2 và 3n + 11 là hai số nguyên tố cùng nhau, thì n chia cho 5 dư 0, 1, 2, 4 hay n = 5k, n = 5k +1, n = 5k + 2, n = 5k + 4.
Đúng 0
Bình luận (0)
Số các số hạng của S là: \(\frac{\left(2n-1-1\right)}{2}+1=n-1+1=n\).
S = 1 + 3 + 5 + ........ (2n - 1)
\(=\frac{\left(2n-1+1\right).n}{2}=n.n=n^2\).
Suy ra S là một số chính phương.
Đúng 0
Bình luận (0)
1 Khi nào thì ta nói số tự nhiên a chia hết cho số tự nhiên b
2 Phát biểu và viết dạng tổng quát hai tích chất chia hết của một tổng
3 Phát biểu các dấu hiệu chia hết cho 2,3,5,9
4 Thế nào là số nguyên tố ,hợp số? Cho ví dụ
5 Thế nào là 2 nguyên tố cùng nhau ? cho ví dụ
1 a chia hết cho b khi a là bội của b
b là ước của a
2 a chia hết cho m, b chia hết cho m
=> (a+b) chia hết cho m
a chia hết cho m, b chia hết cho m, c chia hết cho m
=> (a+b+c) chia hết cho m
3 Dấu hiệu chia hết cho 2 là những số có tận cùng là 0,2,4,6,8
Dấu hiệu chia hết cho 3 là những số có tổng chia hết cho 3
Dấu hiệu chia hết cho 5 là những số có tận cùng là 0 hoặc 5
Dấu hiệu chia hết cho 9 là những số có tổng chia hết cho 9
4 số nguyên tố là số tự nhiên >1, chỉ có 2 ước là 1 và chính nó
VD 47
hợp số là số tự nhiên >1, có nhiều hơn 2 ước.
VD 8
5 2 số nguyên tố cùng nhau là 2 số có ƯCLN bằng 1
VD 2 và 3
Đúng 0
Bình luận (0)




















